Coherence resonance in influencer networks

Ralf Tönjes, Carlos E. Fiore, Tiago Pereira

https://doi.org/10.1038/s41467-020-20441-4, Volume: 12, Pages: null

Article Type: research-article Article History

Publisher: Nature Publishing Group UK

- Facebook
- Twitter
- Linkedin
- Whatsapp
Altmetric

Table of Contents

Introduction
Results
Discussion
Methods
Supplementary information
Supplementary information

Abstract

Complex networks are abundant in nature and many share an important structural property: they contain a few nodes that are abnormally highly connected (hubs). Some of these hubs are called influencers because they couple strongly to the network and play fundamental dynamical and structural roles. Strikingly, despite the abundance of networks with influencers, little is known about their response to stochastic forcing. Here, for oscillatory dynamics on influencer networks, we show that subjecting influencers to an optimal intensity of noise can result in enhanced network synchronization. This new network dynamical effect, which we call coherence resonance in influencer networks, emerges from a synergy between network structure and stochasticity and is highly nonlinear, vanishing when the noise is too weak or too strong. Our results reveal that the influencer backbone can sharply increase the dynamical response in complex systems of coupled oscillators.

Influencer networks include a small set of highly-connected nodes and can reach synchrony only via strong node interaction. Tönjes et al. show that introducing an optimal amount of noise enhances synchronization of such networks, which may be relevant for neuroscience or opinion dynamics applications.

Keywords

Applied mathematics, Nonlinear phenomena

Tönjes,Fiore,and Pereira: Coherence resonance in influencer networks

Introduction

A central discovery in network science is that a small group of highly connected hubs can couple to the network more strongly than their peers and greatly influence the network behavior^1–6. Examples of network influencers can be found in neuroscience (e.g., normal and aberrant synaptic connectivity^7–10), political opinions (e.g., election blogging¹¹ or social networks), and man-made scale-free networks (e.g., the internet¹). Surprisingly, the presence of such influencers makes synchronization of deterministic network dynamics more difficult because networks with influencers require stronger coupling than homogenous networks^12,13; indeed, in many situations, synchronization of influencer networks cannot be achieved at all^14,15. This observation is all the more remarkable because synchronization plays a fundamental role in regulating network function^16,17 and is mediated predominantly through influencers^7,18,19. This raises a crucial question: why have many real-world networks evolved to contain influencers when they appear to be detrimental to the network dynamics, at least at face value?

While strong random fluctuations usually have a negative effect in complex systems it has long been recognized that a small amount of noise can actually improve the system response and its ability to process information. Known mechanisms for such a constructive influence of noise are stochastic resonance, coherence resonance and noise induced synchronization^20–30. The term coherence resonance is used to describe an optimal response of noise-induced oscillations without external stimmulus in excitable cells²². It was observed in globally coupled systems²³, in homogeneous networks^24,25, in non-excitable systems near a Hopf bifurcation²⁶ and two coupled oscillators²⁷. The effects of coherence resonance and its role in heterogeneous networks such as influencer networks remains elusive.

In this work, we show that stochastic forcing of influencers can lead to an optimal collective network response. Strikingly, introduction of noise synergizes with the network structure to create collective oscillations that become optimal at a given noise strength in the influencers. This phenomenon emerges in two steps. First, the network acts as a nonlinear filter for the stochastic influencer dynamics, and at an optimal noise strength, the influencers induce synchronization in the nodes directly connected to them. Second, different parts of the network develop macroscopic dynamics and interact indirectly through the influencers. We develop an adiabatic theory to uncover this macroscopic interaction law and show that it mediates the emergence of global collective oscillations. When the noise in the influencers is either too weak or too strong, the coupling vanishes. Interestingly, at a macroscopic level, the interaction between different parts of the network can be described by a hyper-graph.

We refer to a network where most nodes couple predominantly to a small number of influencers as an influencer network, and refer to the remaining nodes as followers (Fig. 1). As generic oscillatory dynamics, we consider a network of phase oscillators

Here, ω_n is the natural frequency of node n, which couples with strength λ_n to the weighted mean of the coupling functions g to neighboring nodes m. Given a network weight coupling matrix W_nm ≥ 0, which is nonzero if node n receives a link from node m, the intensity μ_n is the total coupling weight received by the nth node. A table of parameters and their function is provided in Methods. The coupling

is generic for weakly coupled, nearly identical oscillators^31,32. The parameter α is called phase frustration and the bias c₀ is due to shear, an amplitude dependence of the frequency^33,34. The effect of shear is a shift in the average frequency proportional to the coupling strength. Phase equations with this form of coupling g are known as the Kuramoto-Sakaguchi model^35,36 and are widely applied across scientific disciplines^31–36. In addition, each term

\sqrt{2 D_{n}} ξ_{n}

denotes uncorrelated Gaussian white noise of strengths D_n. In many studies, the coupling strength λ_n to the local mean-field is chosen to be uniform, in which case the coupling is called normalized. In real-world and experimental systems, though, coupling may be heterogenous and hubs can couple more strongly to the network^5,18. We model this coupling as

For simplicity, throughout this exposition we consider the coupling intensity β_n = β, the noise strength D_n = D, and the frequency ω_n = ω, to be identical for all influencers. For the followers we assume a Lorentzian frequency distribution with mean frequency ω₀ and width γ₀. Noise is of identical strength D_n = D₀ in all followers. We denote Δω = ω − ω₀ the average gap in natural frequencies between influencers and followers.

Fig. 1

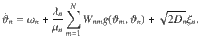
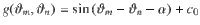
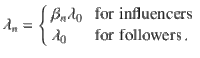
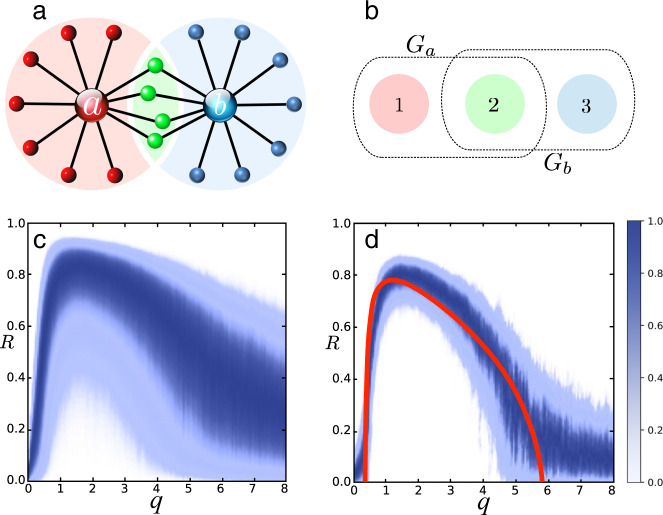
Coherence resonance in an influencer network.

Distribution of the order parameter R versus the effective diffusion q in the influencers. a Influencers a and b are hubs that couple strongly to the network, and all other nodes are regarded as followers. Three distinct partitions of followers are shown in red, blue, and green, which connect to influencer a, b, and both a and b, respectively. In our simulation, each partition has 300 followers. b Mean-field theory predicts that the interactions of the partition mean-fields take place in a hyper-graph mediated by the coupling functions G_a and G_b see Methods. c, d For each value of effective noise strength q in the influencers, we plot the density of the global order parameter R on a color scale from 0 (white) to the maximum value (dark blue). At an optimal noise strength, the mean value of the global order parameter reaches a maximum, revealing the coherence resonance effect. In c the dynamical frequency gap between influencers and followers ΔΩ/λ₀ = 18 is moderate, whereas in d ΔΩ/λ₀ = 198 is large. The solid red line in c is our analytical prediction.

In Methods we show how Eq. (1) can be recast in terms of dimensionless effective parameters shown in Table 1. These effective parameters, and in particular the influencer effective noise strength q = D/ΔΩ, play key roles in the collective dynamics of the system. The dynamical frequency gap ΔΩ/λ₀ leads to a time scale separation between the dynamics of the followers and the influencers. A coupling intensity β of comparable but smaller magnitude leads to an effective coupling strength Λ close to one for which the effect of coherence resonance is most pronounced. We note that the dynamical frequency gap needs to be large in units of λ₀, but it can be small in natural time units. In Supplementary Note 1, we present an example of the transformation for realistic parameters in Eq. (1) to effective parameters.

Table 1

Effective dynamical parameters in influencer networks. We obtain these parameters as described in Methods. These are key parameters in the description of coherence resonance and the optimal noise strength in the influencers.

Parameter	Meaning	range
ΔΩ/λ₀ = Δω/λ₀ + (β − 1)c₀	dynamical frequency gap	ΔΩ/λ₀ ≫ 1
Λ = βλ₀/ΔΩ	dimensionless coupling strength	Λ < 1
q = D/ΔΩ	influencer effective noise strength	q = O(1)
D₀/λ₀	followers effective noise strength	D₀/λ₀ ≪ 1
γ₀/λ₀	followers frequency heterogeneity	γ₀/λ₀ ≪ 1

We divide the followers into partitions P_σ of nodes connected to the same set of influencers. In Fig. 1, we show an influencer network with two influencers (a and b) and three partitions of followers (σ = 1,2,3), which are connected to influencers a, b, or both (see additional examples in Supplementary Note 2). To capture the collective dynamics in each partition σ, we introduce the complex mean-fields

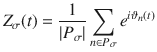
The modulo of the complex mean-field R_σ = ∣Z_σ∣ is the partition order parameter; that is, R_σ = 0 for incoherent, uniformly distributed phases and R_σ = 1 in full synchrony. Similarly, the global mean-field Z and order parameter R are defined by summing over all followers in the network.

Results

With deterministic influencers where q = 0, and when ∣Λ∣ < 1, the influencers cannot frequency lock to the followers. Synchronization of the followers through the influencer backbone is poor and counteracted by noise and frequency heterogeneity in the followers. Our results show that by setting a weak noise strength or frequency heterogeneity in the followers and by changing the effective noise q in the influencers, synchronization of the whole network increases, reaches a maximum, and then decreases.

We numerically integrate our model Eq. (1) in dimensionless units (Table 1) for the network with two influencers (as shown in Fig. 1) with 300 identical followers in each partition, and a small fixed noise strength in the followers. By changing the noise strength in the influencers, we then obtain the distribution of the order parameter R as a function of q. After a transient, the order parameter is independent of the initial conditions. At an optimal noise strength, R reaches its maximum (in expected value), as shown in Fig. 1 for ΔΩ/λ₀ = 18 (panel c) and for ΔΩ/λ₀ = 198 (panel d). The solid line is a theoretical prediction in the thermodynamic limit for heterogeneous followers using a slow-fast approximation. Frequency heterogeneity and noise in the followers have qualitatively and quantitatively the same desynchronizing effect. Optimal synchronization of the whole network is predicted theoretically and achieved in all simulations for an effective noise strength q ≈ 1 in the influencers, see details in Methods. Our mean-field analysis predicts that the effect of coherence resonance is only observed for very small frequency heterogeneity or noise in the followers, below a threshold that depends on Λ (Supplementary Note 3).

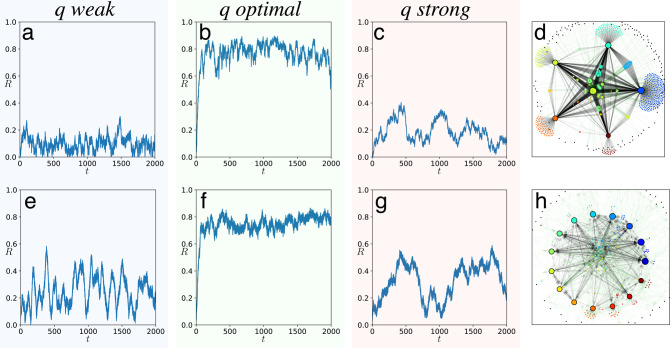
In Fig. 2, we show the time series of the order parameter R for two complex and real-world networks. The upper row represents a scale-free network and the lower row the directed neural network in the model organism Caenorhabditis elegans. We assign the role of influencers to the K most strongly connected nodes and use a weighted connectivity matrix W_nm = 1 for all connections from or to an influencer, and W_nm = 0.01 for all other connections. For small effective noise q in the influencers (Fig. 2, q weak), the order parameter fluctuates at a low level. When q = 1 (q optimal), the order parameter fluctuates around a value close to 1, revealing coherent collective oscillations. Finally, when q is large (q strong), the order parameter decreases again, revealing the loss of synchrony. All parameters for the simulation and numerical scheme can be found in Methods. In Supplementary Note 4, we show three additional examples of coherence resonance in influencer networks; with 3 influencers, a random network with 100 influencers, and a network of linked political blogs.

Fig. 2

Coherence resonance of the order parameter in different complex networks.

a–c, e–g The time series of the order parameter R for three values of noise strength in the influencers for weak q = 0.1 (a, e), optimal q = 1 (b, f), and strong q = 10 (c, g). d, h show the corresponding networks with d a scale-free network with exponent 2¹ and h C. elegans directed neural network³. See Methods for further details. Additional examples can be found in Supplementary Note 5.

Stochastic forcing by a single influencer

Let us consider a single influencer. When its followers are asynchronous, the sinusoidal contributions in the sum of the coupling functions for that influencer average out, and the influencer phase is effectively decoupled from the followers. The influencer is independent of the network and acts as a common stochastic force on the followers connected to it. The additive noise in the influencer enters the dynamics of its followers multiplicatively through the coupling function. That is, the network acts as a nonlinear filter for the noise in the influencers. We can show that the effective diffusion constant of the integrated stochastic forcing in the followers, a proxy for the noise strength, attains a maximum at an optimal effective noise strength

We present the calculations in Methods and further details in Supplementary Note . When oscillations are driven by common multiplicative noise, the effect of noise-induced synchronization can be observed^28–30. As the common noise intensity is increased the oscillators synchronize faster. This suggests that at this optimal value of q the incoherent state will be most unstable. However, behavior of the noise transfer does not explain the synchronization between different partition mean-fields. Because this synchronization requires studying macroscopic dynamics of R far from zero, our next goal is to uncover the interaction function between the mean-fields in different partitions.

Mean-field dynamics of partitions takes place in a hyper-network

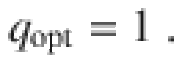
For simplicity, we provide an analysis of the influencer network shown in Fig. 1. Mean-field equations for mixed repulsive and attractive coupling or intra- and inter-partition interactions in the followers can be generalized from these results. In Methods, we show that assuming large partition sizes ∣P_σ∣ ≫ 1, large dynamical frequency gap ΔΩ/λ₀ ≫ 1, and noise free followers D₀ = 0 with frequency heterogeneity γ₀, it is possible to derive averaged dynamics of the partition mean-fields Z_σ in an adiabatic approximation. The resulting deterministic equations have the structure of a hyper-network. In our example, the governing equations are

where the coupling functions are

F describes a Riccati force (see Methods). The weights w_kσ with ∑_σw_kσ = 1 denote the relative size of partition σ among all followers of influencer k. Note that, while in the microscopic description the connections between nodes are pairwise, at the level of mean-fields, edges represented by a coupling function G_k for each influencer can connect multiple partitions of followers. Thus, the mean-field interaction between different parts of the network is described by a hyper-graph.

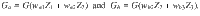
The interaction functions G_a and G_b can be determined analytically; they depend on Λ and q, are maximal at an optimal noise strength, and vanish at critical values of q. That is, at weak or strong noise in the influencers, the hyper-network interactions vanish, revealing the highly nonlinear nature of the phenomenon. In particular, this means that the macroscopic fields will not interact in the strong noise limit. We derive the analytic expressions for the coupling functions G_k(Z; Λ, q) in Methods.

Global synchronization and resonance

When influencers have equal parameters q and Λ the synchronization manifold Z_σ = Z is invariant under (6) and (7) and stable for phase-attractive coupling. Hence, the macroscopic fields synchronize and we can explain the global coherence resonance by restricting the analysis to this invariant subspace. Our mean-field theory predicts both effects: the coherence resonance of the partition order parameters and phase synchronization of the partition mean-fields as shown in Methods. The solid line in Fig. 1 (right) is the stationary average order parameter predicted by our theory in the infinite time-scale separation limit and with frequency heterogeneity γ₀/λ₀ = 0.02 in the followers. The predicted values agree with simulations of the finite size network, large dynamical frequency gap ΔΩ/λ₀ = 198 and identical followers with noise D₀/λ₀ = 0.02. In Supplementary Information, we provide two short movies displaying synchronization of the network in Fig. 1 at an optimal noise strength in the two influencers.

Discussion

We have found a new effect induced by a synergy between noise and network structure to generate a transition towards a synchronization that would not be possible in the absence of noise. The key element for this effect is the existence of influencers – a group of hubs that couple strongly and connect different parts of a network. Although deterministic network parameters prevent synchronization, we show that an optimal noise strength in the influencers can induce and mediate synchronization. The mechanism for this coherence resonance in influencer networks is different from the known effect of coherence resonance in homogeneous networks with excitatory dynamics, where noise simply excites oscillations^23–25. At the macroscopic level, the interaction between different parts of the network is indirect and takes place on an emerging hyper-network, thus changing the interaction structure from the microscopic level. Such higher order interactions have previously been conjectured and reported in neuronal data recordings³⁷. Our findings suggest that the emergent order in complex systems could be controlled by regulating the noise in only a few key nodes.

Methods

Canonical form

To bring the Eq. (1) into a dimensionless form with effective parameters given in Table 1, we change the time scale to units of 1/λ₀ and add the frequency shift from the bias c₀ in the coupling function to the natural frequencies of the oscillators, i.e., ω_n ↦ ω_n + λ_nc₀ and $g (ϑ_{m}, ϑ_{n}) \to \sin (ϑ_{m} - ϑ_{n} - α)$ . The difference between the average follower frequency and the frequency of an influencer, both including the frequency shift from the coupling bias, is the dynamical frequency gap ΔΩ/λ₀ (in units of λ₀). Observing the invariance of the phase equations under a global phase shift, i.e., ϑ → ϑ − ω₀t, we can go into a co-rotating reference frame where the average follower frequency is zero. The deviations of the follower frequencies from their mean frequency ω₀ may be written as γ₀ν_n where the ν_n are taken from some standard distribution with mean zero and the factor γ₀≥0 characterizes the frequency heterogeneity. Then the phase equations for the followers in the new time units and co-rotating reference frame are

and for the influencers with phases ψ_k

Here, Λ_k = λ_k/ΔΩ_k is the ratio between the coupling strength and the frequency of the influencer. In the noise free case, phase locking is only possible for ∣Λ_k∣ > 1. Changing Λ can lead to a discontinuous, explosive synchronization^12,38. The terms

{\tilde{ξ}}_{m}

are independent white noise with

⟨ {\tilde{ξ}}_{m} (t) {\tilde{ξ}}_{n} (t^{'}) ⟩ = δ_{m n} δ (t - t^{'})

in the new units of time and q_k is the effective noise strength in the influencers on the fast time scale ΔΩ_k/λ₀. In Supplementary Note , we provide examples of such rescaling.

Parameters and their meaning

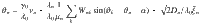
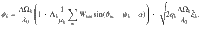
In Table 2, we present the main parameters that naturally appear in the phase model Eq. (1) and give rise to effective parameters, as shown in Table 1 in the main text. The main parameters in our mean-field analysis are shown in Table 3.

Table 2

Parameters in the model presented in Eq. (1) of the main manuscript.

Parameter	Meaning
ω_n	isolated frequency of the nth oscillator;
	set as ω_n = ω₀ + γ₀ν_n for followers and ω for influencers
ω₀	mean frequency of the followers
γ₀ν_n	frequency deviation ω_n − ω₀ of the nth follower
γ₀	scale parameter of follower frequency distribution
Δω	gap (ω − ω₀) between influencer and average follower frequency
W_nm	nonnegative matrix of connection weights
μ_n	connection intensity (μ_n = ∑_mW_nm)
λ_n	coupling strength of the nth oscillator;
	λ₀ for followers and βλ₀ for influencers
β	coupling intensity for influencers
D_n	noise strength set as D for influencers and D₀ for followers
α	phase frustration in the coupling function g
c₀	shear parameter in the coupling function g

Table 3

Parameters of the mean-field analysis presented in Eq. ().

Parameter	Meaning
P_σ	follower partitions according to the influencers they connect to
I_σ	set of influencers of a partition σ
Z_σ	complex mean-field of partition σ (order parameter R_σ = ∣Z_σ∣)
G_k	coupling function between mean-fields mediated by influencer k
w_kσ	relative size of partition σ among the followers of influencer k
F	Ricatti vector field see Eq. (15)
h_σ, h_k	forces on oscillators in partition σ and on influencer k
H_σ	average of h_σ obtained from adiabatic mean-field approximation

Simulations and parameter values

In our analysis and our simulations, we use the transformed, dimensionless canonical form (8) and (9) of the phase equations (1). Existing connections in the network from and to the influencers are given the weight W_mn = 1 and connections between followers W_nm = 0.01. The followers couple to their neighbors with strength λ_n = λ₀ and influencers with strength λ_k = βλ₀. The phase frustration in the coupling function is set to α = −0.1. The frequency deviations ν_n of the followers are drawn from a Cauchy distribution p(ν) = 1/π(ν² + 1) and multiplied by γ₀/λ₀. Thus, frequency heterogeneity and noise strength in the followers are given by γ₀/λ₀ and D₀/λ₀, respectively. We chose β_k = β, λ_k = βλ₀ and D_k = D for all influencers, so that ΔΩ/λ₀, Λ and q are identical for all influencers. We integrate the Langevin equations of the phases with an Euler-Maruyama scheme and small time steps dt = 5 ⋅ 10⁻⁴ because of the large time scale separation ΔΩ/λ₀ ≫ 1.

The parameters of Fig. 1 are as follows: The network structure is a pure influencer network without connections between followers or between influencers. We simulate 300 identical followers γ₀/λ₀ = 0 in each of the three partitions with small independent noise D₀/λ₀ = 0.02. In the lower left panel we have β = 10, a dynamical frequency gap of ΔΩ/λ₀ = 18 and an effective influencer coupling strength Λ = 10/18. In the lower right panel β = 100, ΔΩ/λ₀ = 198 and Λ = 100/198. For each value of the effective influencer noise strength q = D/ΔΩ we record a histogram of the order parameter over T = 10⁴ time units, which is much longer than the relaxation time of R. The theoretical prediction, the solid line in the lower right panel, is for noiseless followers D₀ = 0 and γ₀/λ₀ = 0.02.

Parameters of Fig. 2 are as follows: For the C. elegans directed neuronal network³, we choose the top K = 15 out-degree nodes as influencers. All nodes with zero in-degree have been removed, resulting in a network with N = 268 nodes. Connections between followers are given the weight W_nm = 0.01. We simulate identical followers γ₀/λ₀ = 0 with small independent noise D₀/λ₀ = 0.02. The dynamical frequency gap between followers and influencers is ΔΩ/λ₀ = 18 and the effective coupling strength in the influencers is Λ = 10/18. Shown are three time series of the network order parameter for small (q = 0.1), optimal (q = 1), and large (q = 10) noise strength in the influencers. The undirected scale-free network with exponent 2 is the largest connected component of a network generated via a configurational algorithm¹ without self loops or double edges. We chose the top 5 degree nodes as influencers. The other parameters are the same as in the C. elegans neuronal network.

Mean-field dynamics in influencer networks

We have developed a mean-field theory for undirected influencer networks with connections exclusively between influencers and followers, as shown in Fig. 1. This theory can be generalized to more complex configurations, heterogenous influencers, directed, attractive, or repulsive coupling between followers and influencers, within partitions or between different partitions. While these generalizations may lead to more complex dynamic behavior, the mechanism for the coherence resonance is apparent in the simplest model.

We consider the network as a union of a set P of followers and a set I of influencers. The nodes n connected to an influencer k are elements n ∈ P_k of the periphery of the influencer k. Intersections of the sets P_k form equivalence classes or partitions P_σ of followers that are connected to the same subsets I_σ of influencers such as in Fig. 1 all followers connected to influencer a or b or to both influencers. The phases of the oscillators are encoded as complex variables $z_{n} = \exp (i ϑ_{n})$ for the followers and $z_{k} = \exp (i ψ_{k})$ for the influencers. The dynamics can be formulated in terms of partition averages and averages over the influencers of these partitions

Here, h_σ and h_k are the forces acting on the followers in partition σ and on the influencer k. The weight w_kσ is the relative size of partition σ in the periphery of an influencer k; that is, w_kσ = ∣P_σ∣/∣P_k∣ when P_σ ⊆ P_k or w_kσ = 0 otherwise. Thus, the phase dynamics () and () can be written in complex form as

The first reduction of model complexity is via the Ott-Antonsen approach³⁹ for followers without Gaussian white noise but frequency heterogeneity γ₀/λ₀ with Cauchy-distributed frequency deviations ν_n. In the thermodynamic limit ∣P_σ∣ → ∞ (keeping the ratios w_kσ of the partition sizes constant) there exists a globally attractive invariant manifold on which the mean-fields Z_σ evolve by a complex Riccati equation as

For large partition sizes, Eqs. ()–() provide a good description of the system dynamics, including an accurate description of the fluctuations of the mean-fields (see Supplementary Note ). The effect of small noise D₀/λ₀ in the followers is comparable to the effect of frequency heterogeneity γ₀/λ₀. For small white noise, the Ott-Antonsen manifold is no longer invariant but one can derive a hierarchy of corrections to the dynamics () in increasing orders of the noise strength. To the zeroth order the effects of frequency heterogeneity and noise are identical⁴⁰. In fact, if the noise in the followers is white Cauchy noise, the equivalence of noise and frequency heterogeneity is exact⁴¹.

Slow-fast dynamics

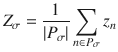
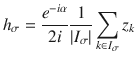
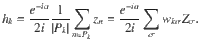
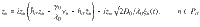
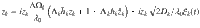
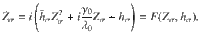
If there is a large dynamical frequency gap ΔΩ_k/λ₀ ≫ 1 between the followers and an influencer, oscillators in the follower group experience an average force from the fast influencer. Conversely, if the followers are desynchronized, the mean-field of the followers vanishes and the influencer phases perform a drift diffusion process on the circle

whereas the followers connected to only that influencer experience a stochastic forcing by the influencer phase

This forcing is multiplicative since

\sin (ψ_{k} - ϑ_{n} - α) = s_{k} \cos ϑ_{n} - c_{k} \sin ϑ_{n}

with two uncorrelated but not independent random processes

s_{k} (t) = \sin (ψ_{k} - α)

and

c_{k} (t) = \cos (ψ_{k} - α)

. The diffusion constants D_s and D_c for the integrated stochastic forces quantify an effective noise strength and can be calculated as the integral of the respective autocorrelation functions⁴²

We present the details in Supplementary Note . By changing the noise strength D_k, the effective noise strengths D_s and D_c have a maximum at D_k = ΔΩ_k or q_k = D_k/ΔΩ_k = 1. At this noise value, and for incoherent followers, the effect of noise-induced synchronization²⁹ is expected to be strongest. As the amplitudes of s_k and c_k are bounded, when D_k or the time scale separation ΔΩ/λ₀ are further increased the effective noise strengths go to zero.

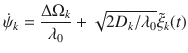
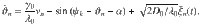
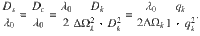
For ΔΩ/λ₀ ≫ 1, the system has slow and fast dynamics and we can replace the influencer phases z_k contributing to the force fields h_σ(11) in each partition σ by the expected values G_k of z_k subject to Langevin equation (14). On the fast time scale of the influencers, the fields h_k are changing very slowly and can assumed to be constant for the calculation of the G_k. In this averaged dynamics, the influencers create an average force H_σ that follows the partition mean-fields adiabatically. The slow dynamics of the partition mean-fields is thus given as

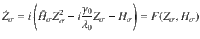
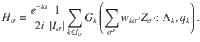
This corresponds to a hyper-graph with partitions σ as nodes and coupling functions G_k for each edge k of the hyper-graph. General setups can be considered as well, with intra and inter-partition coupling and connections between influencers. The absence of such connections shows that the synchronization is indeed a noise-induced effect.

Mean-field of the fast influencers

The Langevin equation (14) for z_k with constant fields h_k is indeed a complex formulation of the noisy Adler equation⁴²

The expected value G of

z = \exp (i ψ)

is the first circular moment of the stationary distribution which has an expression as a continued fraction⁴² and evaluates to a ratio of confluent hypergeometric limit functions ₀F₁(o, x)⁴³. It can be derived from the Fokker-Planck equation noting that the Fourier modes

p_{k} = ⟨ \exp (i k ψ) ⟩

of the stationary distribution p^st(ψ) are in a tridiagonal recurrence relation

which is solved by a continued fraction. Defining q = D/ΔΩ and

we have G = p₁ and

Synchronization manifold and prediction of order parameter

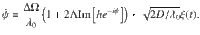
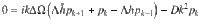
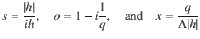
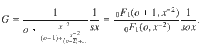
If all influencers have the same effective noise strength $q = q_{k} = \frac{D_{k}}{Δ Ω_{k}}$ and the same effective coupling strength $Λ = Λ_{k} = \frac{β λ_{0}}{Δ Ω_{k}}$ , the synchronization manifold where all partitions have identical mean-fields Z_σ = Z = R^iΘ is invariant under the averaged dynamics (19) and (20) on the hyper-graph and we can write

where G(Z; Λ, q) is defined as () with

In particular, because of rotational symmetry, the dynamics of the amplitude R = ∣Z∣ does not depend on the angle Θ of the mean-field

If the synchronization manifold is stable, the stable fixed points of this dynamics where

\dot{R} = 0

approximate the average order parameter over all followers. From () we find that the level sets of the right-hand side of

determine this average order parameter R for any given γ₀/λ₀ implicitly. We show this prediction for γ₀/λ₀ = 0.02 and Λ = 0.51 as a solid line in the lower right panel in Fig. 1. Further resonance curves and maxima of R for different heterogeneities γ₀ and different Λ can be found in Supplementary Note .

Peer review information: Nature Communications thanks Anna Zakharova, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

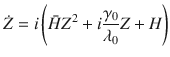
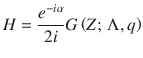
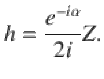
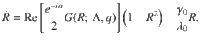
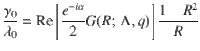
Supplementary information is available for this paper at 10.1038/s41467-020-20441-4.

Acknowledgements

We would like to thank C. Sagastizábal, D. Eroglu, S. van Strien, D. Turaev, J. Lamb, and A. Pikovsky for enlightening discussions. This work was supported in parts by the DFG and FAPESP through the IRTG 1740/TRP 2015/50122-0, by the Center for Research in Mathematics Applied to Industry (FAPESP Cemeai grant 2013/07375-0) and grants 2015/04451-2, by the Royal Society London, CNPq grant 302836/2018-7, and by the Serrapilheira Institute (Grant No. Serra-1709-16124).

Author contributions

R.T. and T.P. wrote the text and developed the theory. R.T. made the slow fast approximation and numerical solutions of the special functions. C.E.F. made simulations of Fig. 1. T.P. and R.T. made the Figures.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Code availability

Input files or sets of input parameters for Fortran as well as self-developed Python codes are available from the corresponding author upon request.

Competing interests

Authors declare no competing interests.

References

Newman

MEJ

Oxford University Press

X-K

, Zhang

, Small

. Rich-club connectivity dominates assortativity and transitivity of complex networks.

doi: 10.1103/PhysRevE.82.046117

Watts

, Strogatz

. Collective dynamics of ‘small-world’networks.

doi: 10.1038/30918

van den Heuvel

, Sporns

. Network hubs in the human brain.

doi: 10.1016/j.tics.2013.09.012

Song

, Sjöström

, Reigl

, Nelson

, Chklovskii

. Highly nonrandom features of synaptic connectivity in local cortical circuits.

doi: 10.1371/journal.pbio.0030068

Fulcher

, Fornito

. A transcriptional signature of hub connectivity in the mouse connectome.

doi: 10.1073/pnas.1513302113

Bonifazi

. Gabaergic hub neurons orchestrate synchrony in developing hippocampal networks.

doi: 10.1126/science.1175509

Schneidman

, Berry

, Segev

, Bialek

. Weak pairwise correlations imply strongly correlated network states in a neural population.

doi: 10.1038/nature04701

Buzsáki

, Mizuseki

. The log-dynamic brain: how skewed distributions affect network operations.

doi: 10.1038/nrn3687

10.

Gal

. Rich cell-type-specific network topology in neocortical microcircuitry.

doi: 10.1038/nn.4576

11.

Adamic, L. A. & Glance, N. The political blogosphere and the 2004 us election: divided they blog. In Proceedings of the 3rd international workshop on Link discovery, 36-43 (2005).

12.

Zou

, Pereira

, Small

, Liu

, Kurths

. Basin of attraction determines hysteresis in explosive synchronization.

doi: 10.1103/PhysRevLett.112.114102

13.

Rodrigues

, Peron

TKD

, Ji

, Kurths

. The kuramoto model in complex networks.

doi: 10.1016/j.physrep.2015.10.008

14.

Pereira

, van Strien

, Tanzi

. Heterogeneously coupled maps: hub dynamics and emergence across connectivity layers.

doi: 10.4171/JEMS/963

15.

Nishikawa

, Motter

, Lai

Y-C

, Hoppensteadt

. Heterogeneity in oscillator networks: are smaller worlds easier to synchronize?.

doi: 10.1103/PhysRevLett.91.014101

16.

Fries

, Reynolds

, Rorie

, Desimone

. Modulation of oscillatory neuronal synchronization by selective visual attention.

doi: 10.1126/science.1055465

17.

Bruno

, Sakmann

. Cortex is driven by weak but synchronously active thalamocortical synapses.

doi: 10.1126/science.1124593

18.

Morgan

, Soltesz

. Nonrandom connectivity of the epileptic dentate gyrus predicts a major role for neuronal hubs in seizures.

doi: 10.1073/pnas.0801372105

19.

Zamora-López

, Zhou

, Kurths

. Cortical hubs form a module for multisensory integration on top of the hierarchy of cortical networks.

20.

Lindner

, García-Ojalvo

, Neiman

, Schimansky-Geier

. Effects of noise in excitable systems.

doi: 10.1016/j.physrep.2003.10.015

21.

Gammaitoni

, Hänggi

, Jung

, Marchesoni

. Stochastic resonance.

doi: 10.1103/RevModPhys.70.223

22.

Pikovsky

, Kurths

. Coherence resonance in a noise-driven excitable system.

doi: 10.1103/PhysRevLett.78.775

23.

Wang

, Chik

, Wang

. Coherence resonance and noise-induced synchronization in globally coupled hodgkin-huxley neurons.

doi: 10.1103/PhysRevE.61.740

24.

Semenova

, Zakharova

, Anishchenko

, Schöll

. Coherence-resonance chimeras in a network of excitable elements.

doi: 10.1103/PhysRevLett.117.014102

25.

Masoliver

, Malik

, Schöll

, Zakharova

. Coherence resonance in a network of fitzhugh-nagumo systems: Interplay of noise, time-delay, and topology.

doi: 10.1063/1.5003237

26.

Ushakov

. Coherence resonance near a hopf bifurcation.

doi: 10.1103/PhysRevLett.95.123903

27.

Amro

, Lindner

, Neiman

. Phase diffusion in unequally noisy coupled oscillators.

doi: 10.1103/PhysRevLett.115.034101

28.

Nakao

, Arai

, Kawamura

. Noise-induced synchronization and clustering in ensembles of uncoupled limit-cycle oscillators.

doi: 10.1103/PhysRevLett.98.184101

29.

Pimenova

, Goldobin

, Rosenblum

, Pikovsky

. Interplay of coupling and common noise at the transition to synchrony in oscillator populations.

doi: 10.1038/srep38518

30.

Dolmatova

, Goldobin

, Pikovsky

. Synchronization of coupled active rotators by common noise.

doi: 10.1103/PhysRevE.96.062204

31.

Acebrón

, Bonilla

, Vicente

CJP

, Ritort

, Spigler

. The kuramoto model: A simple paradigm for synchronization phenomena.

doi: 10.1103/RevModPhys.77.137

32.

Stankovski

, Pereira

, McClintock

, Stefanovska

. Coupling functions: universal insights into dynamical interaction mechanisms.

doi: 10.1103/RevModPhys.89.045001

33.

Montbrió

, Pazó

. Shear diversity prevents collective synchronization.

doi: 10.1103/PhysRevLett.106.254101

34.

T-W

, Ermentrout

. Partially locked states in coupled oscillators due to inhomogeneous coupling.

doi: 10.1103/PhysRevE.78.016203

35.

Sakaguchi

, Kuramoto

. A soluble active rotater model showing phase transitions via mutual entertainment.

doi: 10.1143/PTP.76.576

36.

Omel’chenko

, Wolfrum

. Nonuniversal transitions to synchrony in the sakaguchi-kuramoto model.

doi: 10.1103/PhysRevLett.109.164101

37.

Giusti

, Ghrist

, Bassett

. Two’s company, three (or more) is a simplex.

doi: 10.1007/s10827-016-0608-6

38.

Vlasov

, Zou

, Pereira

. Explosive synchronization is discontinuous.

doi: 10.1103/PhysRevE.92.012904

39.

Ott

, Antonsen

. Low dimensional behavior of large systems of globally coupled oscillators.

doi: 10.1063/1.2930766

40.

Tyulkina

, Goldobin

, Klimenko

, Pikovsky

. Dynamics of noisy oscillator populations beyond the ott-antonsen ansatz.

doi: 10.1103/PhysRevLett.120.264101

41.

Tönjes

, Pikovsky

. Low-dimensional description for ensembles of identical phase oscillators subject to cauchy noise.

doi: 10.1103/PhysRevE.102.052315

42.

Risken

Springer-Verlag

43.

Stratonovich, R. L. Topics in the theory of random noise, vol. 1 (Gordon and Breach, New York, 1963).