Spin transitions in OLEDs under non-perturbative resonant drive

Theoretical treatment of the spin dynamics in a strongly driven electron-hole pair beyond the perturbative regime is extremely challenging and has not been considered in detail previously. We approach this problem using quantum-mechanical Floquet theory³⁰. The electron-hole spin-pair Hamiltonian, H(t), is time dependent owing to the presence of a time-dependent (sinusoidal) driving field. Besides the drive, we incorporate in H(t) the electron and hole spin coupling to the external field B₀ and the effective local internal hyperfine fields, as well as the isotropic exchange and dipolar interactions between the electron and hole spins. Note that, given the exceedingly weak spin-orbit coupling of the organic semiconductor material used in the experiments discussed in the following, the spin Hamiltonian is perfectly defined without an explicit spin-orbit term, using effective Landé g-factors instead. We direct the interested reader to a recent joint experimental and theoretical examination of the influence of spin-orbit coupling in these materials¹⁴. Although all these interactions are time independent, the local hyperfine fields and the dipolar interaction are taken to be random and different for different configurations. Further details of the statistical distribution of spin pairs and the numerical approach to account for this are discussed in Supplementary Notes 1.5 and 1.6.

The time-periodic character of the driving field allows us to write the Fourier decomposition of the Hamiltonian as $$ H_{\alpha \beta }\left(t\right)={\sum }_n{H}_{\alpha \beta }^{\left(n\right)}{e}^{in\omega t}$$, where ω is the angular frequency of the incident radiation. Here, and in the following, the Greek indices α and β run over the four spin-pair states, the three triplets $$ T_{+},T_0,T_{-}$$ and the singlet S, which are chosen as the spin Hilbert space basis for the subsequent discussion. The Floquet dressed states $$ \left(\mid \alpha ,n\right.⟩$$ with photon number $$ n=0,\pm 1,\pm 2,\dots $$ are defined as the product of the spin Hilbert space basis state α and the Fourier-space basis state |n〉. The dressed states form an orthonormal basis in an infinite-dimensional Floquet Hilbert space. A change of n modifies the dressed state while retaining the same spin-pair component. The time-independent, infinite-dimensional Floquet Hamiltonian H_F is then defined in matrix representation as

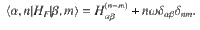
The Floquet approach takes advantage of the fact that H_F is time independent and Hermitian, thus possessing stationary eigenvectors, $$ \mid {\psi }_{\alpha ,n}⟩$$, and real eigenvalues, $$ {\epsilon }_{\alpha ,n}$$. The Floquet Hamiltonian has a periodic structure so that a shift of the indices by the same integer l changes only the diagonal matrix elements

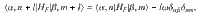
The spin-density matrix of an ensemble of spin pairs, ρ, satisfies the stochastic Liouville equation and is used to compute the steady-state singlet content of the spin pair, i.e., the observable responsible for the experimentally measured conductivity of the OLED. Ultimately, this observable can be expressed by the trace of the steady-state spin-density matrix, $$ \mathrm{tr}{\tilde{\rho }}_0$$, where the tilde indicates the steady-state solution to the stochastic Liouville equation, which is explicitly time dependent because of the time-periodic Hamiltonian, with the index 0 referring to the time-independent Fourier component thereof. As described in detail in Supplementary Note 1.2, from this solution, we can express $$ \mathrm{tr}{\tilde{\rho }}_0$$ through the following phenomenological parameters: the rate of spin-pair generation, G; the spin-pair dissociation rate, r_d; the singlet and triplet recombination rates, r_S and r_T; and the spin-lattice relaxation time, T_sl. For convenience, we introduce a characteristic total decay rate of the pair, $$ w_d=r_d+r_T+1/T_{\mathrm{sl}}$$, and define the difference in singlet and triplet recombination rates $$ k_r=r_S-r_T$$, which determines the overall magnetic-field response of the conductivity. Using $$ \mid {\psi }_{\alpha ,0}⟩$$ as the eigenvectors of the Floquet Hamiltonian and $$ {\mathrm{\Pi }}_S$$ as the projection operator onto the dressed singlet subspace, $$ {\mathrm{\Pi }}_S={\sum }_n\mid \left(S,n\right.⟩\left.⟨S,n\right)\mid $$, we arrive at an expression for the steady-state spin-density matrix as

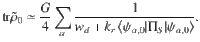
Equation (3) is derived perturbatively, to leading order in the small difference of singlet and triplet recombination rates k_r. Note that $$ k_r\ll ∣D∣,∣J∣$$, where D and J are the average dipolar and exchange interactions between electron and hole spins within the pairs. Further details of this approximation are discussed in Supplementary Note 1.4.

The steady-state device current measured in an experiment is a function of the static and oscillating magnetic fields, which give rise to a change $$ \mathrm{\Delta }I\left(B_0,B_1\right)=I\left(B_0,B_1\right)-I\left(B_0,0\right)$$ of the spin-dependent OLED current, i.e., the magnetic resonance. This steady-state spin-dependent device current probed in experiments corresponds to the average of $$ \mathrm{tr}{\tilde{\rho }}_0$$ over all the random distributions of local hyperfine fields and dipolar couplings, i.e. the average over spatial orientations of electronic spin pairs with respect to the applied magnetic field,

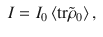
We utilize Eqs. (3) and (4) for the numerical calculation of the EDMR signal $$ \mathrm{\Delta }I\left(B_0,B_1\right)$$. The Floquet Hamiltonian H_F is determined from Eq. (1), for a randomly generated configuration of local hyperfine fields and dipolar coupling. To approximately calculate the infinite-dimensional eigenvectors $$ {\psi }_{\alpha ,0}$$ of H_F entering in Eq. (3), we truncate the infinite-dimensional Floquet Hamiltonian and the corresponding Hilbert space as described in Supplementary Note 1.3. The truncation procedure consists of restricting the photon numbers by some integer value, N₀, or equivalently restricting the indices m and n in Eq. (1) to run between −N₀ and N₀, where N₀ is determined by the requirements on the accuracy of the numerical procedure. The eigenvectors of the truncated Floquet Hamiltonian are used to evaluate $$ \mathrm{tr}{\tilde{\rho }}_0$$ from Eq. (3). The procedure is repeated multiple times and the field-dependent current is found as the average of the numerical values computed for each random configuration according to Eq. (4).

Diagrammatic representation of hybrid light-matter states

In order to build up an intuitive understanding of the resonant transitions of the electron-hole spin pair emerging under strong and ultrastrong resonance drive and to differentiate the Floquet states responsible for the specific transitions, we develop a diagrammatic representation³¹ of the dressed states $$ \left(\mid \alpha ,n\right.⟩$$. For simplicity, we describe the transitions in terms of effective g-factors of resonances. Obviously, this does not relate to the g-factor of the resonant spins—these are all nearly free electrons—but to the ratio between the driving field oscillation frequency and the frequency corresponding to the Zeeman splitting induced by the static magnetic field B₀. Figure 1a illustrates the fourfold basis of the Floquet states. A resonant transition involving the creation or annihilation of a photon, shown in Fig. 1b, gives rise to an effective resonance in the overall singlet content of the pair at a g-factor g ≈ 2. This resonance arises from a superposition of transitions depicted by an infinite number of diagrams of increasing order. Specific examples of such diagrams describing the g ≈ 1 two-photon resonance owing to simultaneous annihilation or creation of two photons, shown in Fig. 1c, are given in Fig. 1e. The vortices of the diagrams mark transitions in spin state and occur either by photons, marked as dots, or due to magnetic scattering interactions such as hyperfine or dipolar spin-spin coupling (crosses). The entire singlet content of the spin ensemble in the steady state is computed by approximating the infinite summation over all states (see Supplementary Note 1.4). A further group of transitions (Fig. 1d) involves a change of the magnetic quantum number by $$ \mathrm{\Delta }m=\pm 2$$, corresponding to a half-field resonance at g ≈ 4. Since the steady-state singlet content is given by a summation over all spin permutations, resonances at fractional g-factors will also arise as combinations of the different processes.

Fig. 1

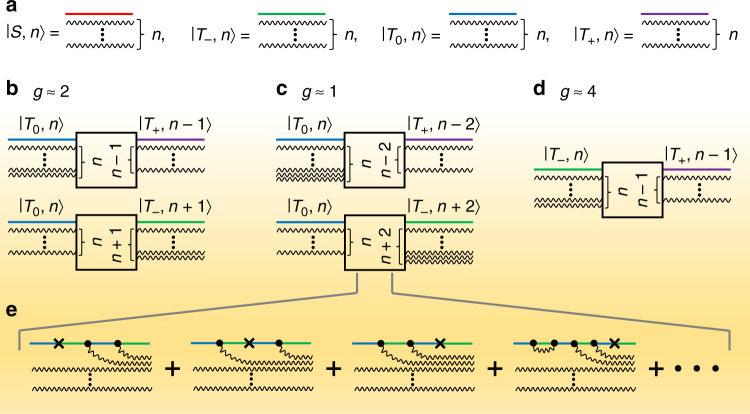
Multiple-quantum transitions of spin pairs in the singlet-triplet basis.

a The Floquet states describing the conductivity of an OLED under magnetic-resonant excitation are defined by the photon number n (illustrated as wavy lines before and after the interaction) and the spin wavefunction (red, green, blue, purple). b The spin-½ resonance of the pair at an effective g-factor of g ≈ 2 corresponds to a raising or lowering of n. c, d Resonances also arise at g ≈ 1 and g ≈ 4 owing to two-photon and half-field transitions, respectively. e Examples of diagrams of the two-photon transitions, where the vortices indicate the creation or annihilation of a photon (•) or spin scattering not involving a photon (×), e.g., owing to hyperfine or dipolar coupling. An infinite number of higher-order loops exists. Magnetoresistance on resonance is calculated by summation over all transitions.

Even though multi-photon transitions in two-level spin systems have been discussed in the context of electron-spin resonance spectroscopy^32–34, these are not analogous to two-photon absorption of electric-dipole transitions. As each photon carries angular momentum $$ \ell =1$$, a $$ \mathrm{\Delta }\ell =2$$ electric-dipole transition requires a final electronic orbital with different angular momentum. A spin-½ system can only undergo $$ \mathrm{\Delta }\ell =1$$ transitions, however, implying that a magnetic-dipole transition by absorption of two identical photons is impossible. Instead, two-photon magnetic-dipole transitions arise with a combination of different photons³⁴ whose magnetic-field components have transversal and longitudinal orientation with regard to the magnetic field B₀.

Computation of the EDMR spectrum as a function of driving strength

In Fig. 2a the calculated change of spin-dependent current $$ \mathrm{\Delta }I\left(B_0,B_1\right)$$ as a function of Zeeman splitting B₀ and driving field amplitude B₁ for an incident radiation frequency of 85 MHz is plotted (see Supplementary Note 1.5 for numerical details). The width of the fundamental resonance g ≈ 2 at low driving fields is defined by the expectation value of the local hyperfine field experienced by electron or hole spins, $$ \mathrm{\Delta }{B}_{\mathrm{hyp}}$$^25,28, as described in Supplementary Note 5. The effective g-factors of the resonant species are indicated on the left-hand field ordinate. Six distinct resonances are seen, with the amplitudes and positions of these depending on B₁. The six features are assigned the Floquet-state transitions marked in the diagram of spin-pair eigenstates in Fig. 2b. Here, states $$ \left(\mid 2\right.⟩$$ and $$ \left(\mid 3\right.⟩$$ depend on the particular nature of the intrapair interaction, i.e., dipolar and exchange coupling (see Supplementary Note 1.1). Three resonances arise from full-field $$ \mathrm{\Delta }m=\pm 1$$ transitions, and three from half-field $$ \mathrm{\Delta }m=\pm 2$$ transitions. Feature (i) is owing to the one-photon spin-½ resonance and initially undergoes power broadening, before splitting due to the AC-Zeeman effect and subsequently inverting in amplitude owing to the spin-Dicke effect²⁴. The g ≈ 1 feature (ii) results from two-photon transitions, and the g ≈ 2/3 feature (iii) from three-photon absorption. Resonances also occur between pure triplet states and result from transitions involving either one (iv) (g ≈ 4), three (v) (g ≈ 4/3), or five (vi) (g ≈ 4/5) photons. Features (i–iii) clearly move towards lower B₀ values with increasing B₁, which is a manifestation of the Bloch-Siegert shift (BSS), discussed in more detail below and in Supplementary Note 6. The BSS of the g ≈ 2 resonance results in merging into a zero-field resonance at high B₁. The resonances appear self-similar, with the AC-Zeeman and spin-Dicke effects apparent in features (i–iii). Crucially, the inversion of ΔI at the onset of the spin-Dicke effect coincides with the formation of a new spin basis of the electromagnetically dressed state²⁴. In this hybrid light-matter state, power broadening of the resonant transition is absent since the electromagnetic field is implicit in the state’s wavefunction²⁵, allowing the BSS to be resolved clearly.

Fig. 2

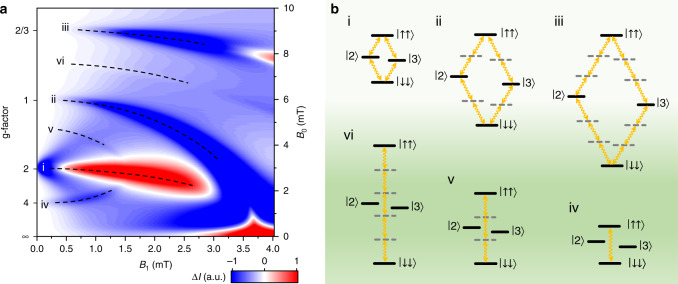
Floquet spin states in OLED magnetoresistance.

a Calculated change of spin-dependent recombination current as a function of static field B₀ and oscillating field B₁ for a frequency of 85 MHz. b Term diagrams of integer and fractional g-factor multi-photon transitions. (i–iii) $$ \mathrm{\Delta }m=1$$ transitions; (iv–vi) $$ \mathrm{\Delta }m=2$$ transitions.

Experimental probing of hybrid light-matter Floquet states in OLED EDMR

Identifying these Floquet states experimentally in the spin-dependent transitions that control the magnetoresistance of OLEDs poses two challenges. First, the effective hyperfine fields must be sufficiently small, such that the different resonances do not overlap spectrally. Hyperfine coupling broadens the resonant magnetic-dipole transition inhomogeneously, making individual microscopic spins distinguishable in terms of their resonance energy. This disorder determines the threshold field for the onset of spin collectivity²⁴, when each individual spin becomes indistinguishable with respect to the driving field. Previous studies of the condition of strong magnetic-resonant drive of OLEDs employed either conventional hydrogenated organic semiconductors^18,24, or partially deuterated materials with reduced hyperfine coupling strengths²⁴. To maximize the resolution of the experiment, we synthesized a perdeuterated conjugated polymer, poly[2-(2-ethylhexyloxy-d₁₇)-5-methoxy-d₃-1,4-phenylenevinylene-d₄] (d-MEH-PPV), with 97% of the protons replaced by deuterons³⁵. Second, OLEDs have to be designed with integrated microwires which generate the oscillating field¹⁸. The smaller the OLED pixel relative to the microwire, which narrows down to a width of 150 μm, the lower the inhomogeneity in both static and oscillating magnetic fields—at the cost of EDMR signal-to-noise ratio. The alternating current passed through the microwire generates heat, requiring careful optimization of electrical and thermal conductivity of the monolithic OLED-microwire device¹⁸.

Figure 3 plots the change ΔI of the steady-state DC forward current I₀ = 500 nA under 85 MHz RF radiation, as a function of B₀ and the square root of the power P of the applied radiation. The dominant Floquet spin state transitions identified in the calculation in Fig. 2 are resolved in the experiment and labeled correspondingly: the power-broadened g ≈ 2 spin resonance which inverts its sign in the spin-Dicke regime with subsequent BSS (i); the two-photon transition and the corresponding BSS of the g ≈ 1 resonance (ii); and the half-field resonance at g ≈ 4 (iv). In principle, $$ \sqrt{P}\propto B_1$$, although heating of the microwire at high powers will change the microwire impedance and therefore increase the uncertainty on the abscissa scale in Fig. 3 (see Supplementary Note 4). From an analysis of the experimentally observed power broadening given in Supplementary Fig. 2, we estimate that B₁ fields of up to 3 mT are reached, consistent with the universal scaling of EDMR amplitude dependence on B₁ with hyperfine field strength as shown in Supplementary Fig. 6. Note that, because the measurements were actually carried out before the calculations were completed, unfortunately, we did not probe the B₀ field region above 7.5 mT, as there was no reason to anticipate additional features appearing there. We will leave experimental exploration of this interesting field region for future studies.

Fig. 3

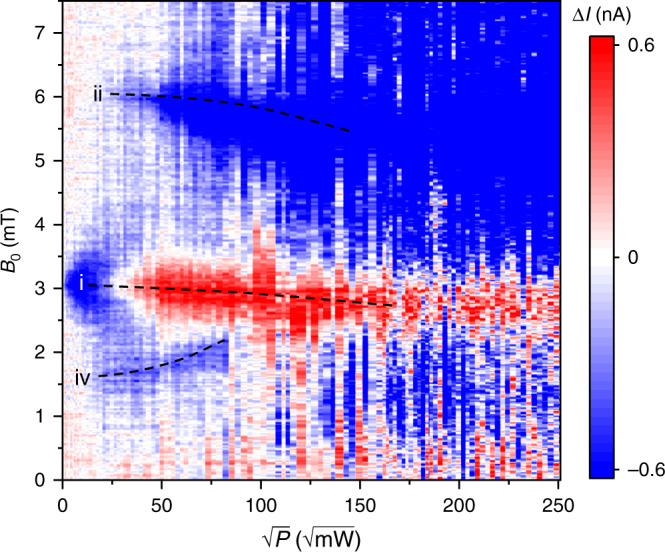
Measured change in spin-dependent OLED current ΔI as a function of driving power.

The dominant features of Fig. 2 are indicated by dashed lines. The relationship $$ \sqrt{P}\propto B_1$$ is confirmed for P ≤ 100 mW (see Supplementary Note 4), but, due to heating-induced resistivity changes of the microwire generating the resonant field, the uncertainty on the abscissa scale increases with higher P.

A simple intuitive rationalization of the intriguing two-photon transition can be formulated. Two-photon transitions between the up and down state of a spin-½ species are dipole forbidden. In analogy to light waves, the resonant radiation can be described in the photon picture. A photon has an angular momentum quantum number of 1 and can assume one of the two projection states of either $$ m=+1$$ or $$ -1$$ relative to the direction of propagation. These so-called $$ {\sigma }^{+}$$ and $$ {\sigma }^{-}$$ photons can be associated with the right and left-hand circularly polarized fields. In a σ-photon state, where the direction of propagation is along the quantization axis, the AC magnetic-field component B₁ is perpendicular to B₀. The absence of a photon state with m = 0 can be traced back to a photon having zero mass. However, a linear AC field B₁ in the direction of quantization, $$ B_1\parallel B_0$$_, is referred to as a π-photon propagating perpendicular to the quantization axis. These unconventional π-photons feature in atomic spectroscopy but are also discussed within a semi-classical picture of magnetic resonance^2,34, and can be thought of as photons of total angular momentum zero. Two-photon transitions are only possible with a combination of σ and π-photons. As the excitation scheme employed here would appear to only involve σ-type photons, it is not immediately obvious how angular momentum is conserved to give rise to the strong two-photon resonances observed in theory and experiment.

Figure 4a provides an intuitive picture for the emergence of the two-photon transition. Transversal oscillating magnetic-field components are orthogonal to B₀, but the latter is superimposed with local static isotropic hyperfine fields. This superposition leads to the effective static magnetic field, B_s, tilted from the z axis by a small but finite angle. Thus, the superposition of B₀ and the local hyperfine fields results in a total static field B_s parallel to one component of the oscillating magnetic field, which is sufficient to enable the $$ \sigma -\pi $$ two-photon transition conserving angular momentum. To test this picture, in a separate experimental setup described in the Methods section, we probed the angular dependence of the g ≈ 1 resonance. The complete quantum-statistical simulation of the effect using the Floquet ansatz described above predicts a $$ \sin 2\alpha $$ dependence, in agreement with the geometric arguments forward above. The characteristic features of the prediction from theory are matched by the experimental data as shown in Fig. 4b. To allow the angle to be swept, these experiments were performed at a very low B₀ of 780 μT corresponding to a resonance frequency of 22 MHz.

Fig. 4

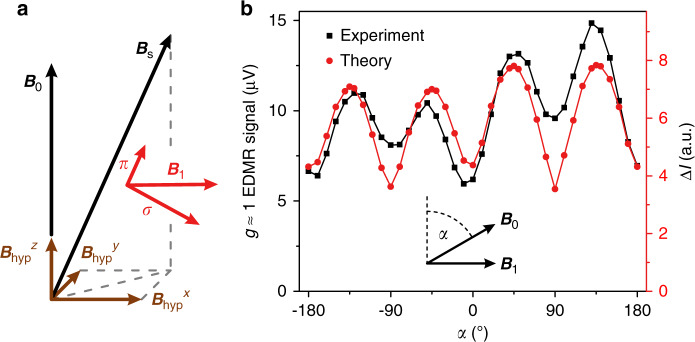
Intuitive rationalization of the two-photon transition and the angular dependence of the two-photon g ≈ 1 EDMR signal.

a Sketch of the magnetic-field configuration acting on a spin within a spin pair. Oscillating magnetic-field components (red arrows) parallel (π) and perpendicular (σ) to the effective local quantizing static magnetic field B_s arise from the decomposition of B₁ with respect to the total static magnetic field that results from the superposition of B₀ and B_hyp. b Angular dependence of the two-photon EDMR resonance measured at f = 22 MHz (black) for the d-MEH-PPV devices. The experimental results match the $$ \sin 2\alpha $$ dependence predicted by theory (red). Lines are a guide to the eye.

Two-photon resonances arise both under parallel and perpendicular excitation. This observation can be explained by the illustration in Fig. 4a: photons of both longitudinal (π) and transversal (σ) polarizations exist even for parallel or perpendicular field configurations. The lower B₀, the greater the contributions of the transversal hyperfine fields and the influence of dipolar coupling of spins within the spin pairs, which enable the resonances under fully parallel and perpendicular excitation. We note that a slight asymmetry in the angular dependency can be attributed to additional resonant contributions of the second harmonic of the RF signal generated by the RF amplifier. This second harmonic can be removed by filtering the incident RF radiation using a low-pass filter. Alternatively, we replicate this asymmetry in the calculation in Fig. 4b by introducing a second harmonic resonant contribution amounting to $$ ~0.01B_1$$. The additional slight asymmetry in the measurement between, e.g., 45° and 135° is also observed for the fundamental resonance (not shown). This deviation presumably arises from the fact that the RF radiation generated by the stripline is not perfectly linearly polarized.

Device fabrication

In order to establish and detect ultrastrong electron-spin magnetic resonance drive conditions, we developed a new monolithic OLED device structure with an integrated RF microwire. These small circular (57 µm diameter) single-pixel OLEDs allow for bipolar charge-carrier injection using electron and hole injector layers on top of an electrically and thermally separated thin-film wire capable of producing RF magnetic fields B₁ when connected to an RF source. The wire itself runs across the substrate and is shrunk down to 150 μm width beneath the OLED pixel. Details of the layer sequence necessary to achieve electrical and thermal decoupling are given in ref. ¹⁸. Further details can be found in Supplementary Note 2. The active polymer, d-MEH-PPV, was dissolved in toluene at a concentration of 4.5 g/L at a temperature of 50–70 °C and deposited by spin-casting at 800 rpm, as described in ref. ³⁵. The layer was sandwiched as a 100 nm thin film between a Ca/Al stack for electron injection and a TiO₂ (3 nm)/Au (80 nm)/Ti (10 nm) layer covered with PEDOT:PSS (Ossila Al 4083) for hole injection. The structure is comparable to that used in previous studies of the strong-drive regime, where a different π-conjugated polymer with much larger resonance linewidths was used²⁴. For the study presented here, the active-layer material, the layer stack, and the pixel device geometry were redesigned and optimized in order to allow for larger B₁/B₀ ratios to be reached. The monolithic single-pixel OLED device was made following a preparation and deposition protocol as illustrated in Jamali et al.¹⁸ with the following changes: (i) the active polymer layer where the electron-hole pair recombination takes place was nominally 100 nm thick, consisting of spin-coated perdeuterated d-MEH-PPV; (ii) the sample template preparation included placing the silicon wafer in a dry thermal oxidation furnace at 1000 °C for 78 min, producing a 50 nm SiO₂ layer on top of the Si wafer for insulation and better adhesion of the subsequent layer (amorphous SiN); and (iii) an entirely different lateral layout of the templates (cf. Supplementary Fig. 1a) was used compared to that described in Jamali et al.¹⁸, providing larger separation between the electrical contacts of the thin-film wire RF source and the device electrodes in order to avoid cross-talk at high RF powers and minimize heating of the OLED during the room temperature measurements. A photograph of the pixel device template is shown in Supplementary Fig. 1a with the pixel located at the image center. An example of the current-voltage characteristics of the device at room temperature is also given in Supplementary Fig. 1b.

Ultrastrong-drive EDMR spectroscopy

The OLED was subjected to a static magnetic field B₀ and irradiated with RF radiation with in-plane amplitude B₁ using an Agilent N5181A frequency generator and an ENI 510 L RF power amplifier as illustrated in Supplementary Fig. 1a. At the same time, a steady-state electric current was induced with a V = 2.8 V bias using a Keithley voltage source. A Stanford Research (SR570) current amplifier was used to detect changes $$ \delta I$$ of the steady-state forward current of I₀ = 500 nA with and without the RF radiation applied. Measurements of $$ \mathrm{\Delta }I\left(B_0,\sqrt{P}\right)$$ as a function of B₀ and the square root of the applied microwave power P (which is proportional to B₁) were then obtained, as shown in Fig. 3. Further details of the measurement procedure and the determination of the $$ \sqrt{P}$$ to B₁ conversion factor through power broadening are given in the Supplementary Notes 3–7.

Angle-dependent EDMR spectroscopy of the two-photon transition

The angle-dependence measurements of the two-photon resonance were performed in a separate low-field setup with different OLED samples, described in detail in refs. ^5,42. These OLEDs were much larger, with a pixel area of 3.5 mm². RF excitation generated by an Anritsu MG3740A signal generator and amplified by a HUBERT A 1020 RF amplifier was applied to the sample through a coplanar stripline designed to match a 50 Ω impedance. In contrast to the measurements on the monolithic OLED-microwire structures, these experiments were performed under constant-current conditions with $$ I=250\mathrm{\mu }\mathrm{A}$$ applied by a Keithley 238 source-measure unit, so that the EDMR signal corresponds to a voltage measurement. Lock-in detection with a Stanford Research Systems SR830 DSP lock-in amplifier and 100% modulation of the RF amplitude at a frequency of 232 Hz was employed. We used a 3D array of Helmholtz coils (Ferronato BH300-3-A), each supplied by a CAEN ELS Easy-Driver 0520. This allowed us to perform sweeps of B₀ from −2 to +2 mT with an arbitrary orientation of the field vector. Owing to the limited magnetic-field range of the 3D Helmholtz-coil set, we resorted to a lower excitation frequency of 22 MHz with $$ B_1\approx 200\mathrm{\mu }\mathrm{T}$$.