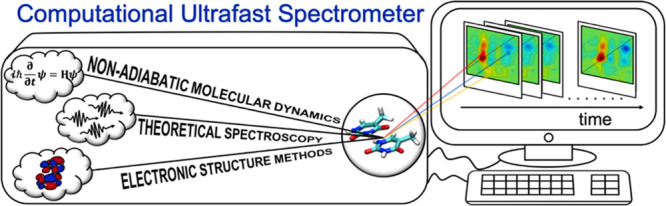
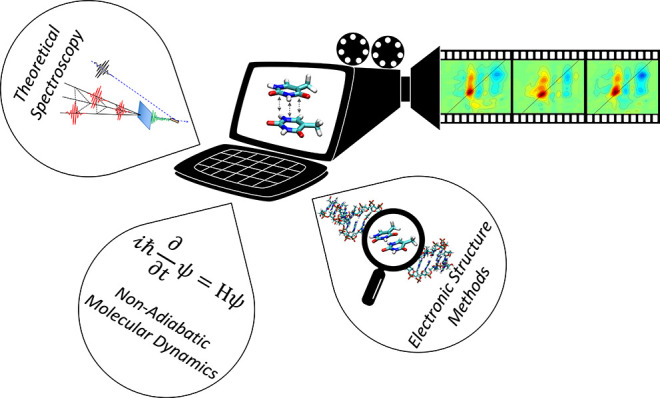
Computational spectroscopy is becoming a mandatory tool for the interpretation of the complex, and often congested, spectral maps delivered by modern non-linear multi-pulse techniques. The fields of Electronic Structure Methods, Non-Adiabatic Molecular Dynamics, and Theoretical Spectroscopy represent the three pillars of the virtual ultrafast optical spectrometer, able to deliver transient spectra in silico from first principles. A successful simulation strategy requires a synergistic approach that balances between the three fields, each one having its very own challenges and bottlenecks. The aim of this Perspective is to demonstrate that, despite these challenges, an impressive agreement between theory and experiment is achievable now regarding the modeling of ultrafast photoinduced processes in complex molecular architectures. Beyond that, some key recent developments in the three fields are presented that we believe will have major impacts on spectroscopic simulations in the very near future. Potential directions of development, pending challenges, and rising opportunities are illustrated.
Time-resolved optical spectroscopy is a versatile tool for resolving dynamic processes in molecules both in their ground and excited electronic states. Since the pioneering microsecond flash photolysis experiments,1 the generation of ever shorter pulses has furnished researchers with an arsenal of techniques enabling them to access faster and faster timescales, spanning from the nanosecond to the attosecond domains (see, e.g., refs (2a) and (2b)). These technological advances have facilitated the study of a broad variety of physical phenomena, from the slowest such as protein conformational changes to the fastest such as electronic dynamics within molecules.
However, it is often not straightforward to interpret the measured time-dependent observables and associate them to specific photophysical/photochemical processes. To address this issue, the progress in experimental techniques has been matched by spectacular advances in ab initio computational methods, which now enable one to study complex molecular systems and to reproduce with nearly quantitative accuracy the measured transient spectra. Theoretical modeling is crucial because it provides the link between the observables and the underlying molecular dynamics, allowing the researcher to interpret the experimental data and to extract from them the maximum amount of information.
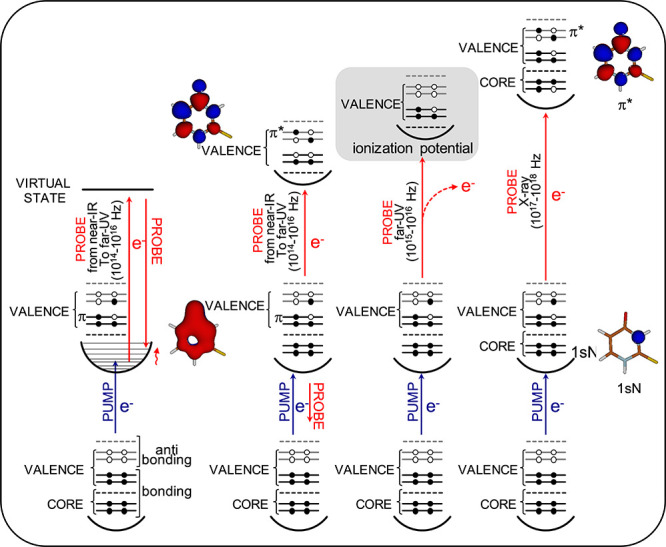
This work summarizes some of the most recent developments and results in first-principles modeling of ultrafast spectroscopy of photoinduced processes in complex molecular systems. We show that computational spectroscopy is a mandatory tool for the interpretation of the complex spectral maps delivered by multi-pulse techniques. We consider light pulses spanning different spectral ranges, from 1014–1016 Hz (NIR-Vis-UV), resonant with optical transitions between the valence electronic states of the chromophores up to their photoionization limit, to 1017–1018 Hz (X-rays), which excite core electrons and possess atomic specificity (see Scheme 1). These pulses cover timescales ranging from the attosecond to the picosecond. We discuss experiments performed within the weak-field perturbative regime. Out of the scope of this Perspective are strong electric fields, attosecond electron dynamics, ground-state structural and solvation dynamics, and solid-state spectroscopy, while time-resolved vibrational spectroscopy techniques are limited to transient stimulated Raman scattering.
Non-linear Multi-Pulse Techniques
Time-Resolved Multi-Pulse Optical Spectroscopy Simulations: Three Distinct Grand Challenges
First-principles simulations of time-resolved optical spectroscopy pose three distinct Grand Challenges (see Scheme 2), whose interplay is required to deliver the full picture:
(1)Light–matter interactions need to be modeled. This is the task of Theoretical Spectroscopy, which describes both the perturbation of the electronic density due to the initial photoexcitation (the pump) and the subsequent interaction of the system under study with a delayed light pulse (the probe).
(2)The field-free evolution of the photoexcited system needs to be described by solving the time-dependent Schrödinger equation for the electrons and the nuclei. This is the field of Non-Adiabatic Molecular Dynamics, i.e., propagation of the nuclear wavepacket on the manifold of photochemically relevant electronic states, describing quantum effects like non-adiabatic population transfer, wavepacket splitting, quantum interferences, and tunneling.
(3)Eventually, the potential energy surfaces (PESs) of the electronic states on which the nuclei are moving, and their derivatives and non-adiabatic couplings, need to be obtained by solving the time-independent Schrödinger equation, which is the task of Electronic Structure Methods, whose application range is dictated by the chromophore size.
Each of the three challenges comes with its own problems and bottlenecks: complexity of the spectroscopic experiment to model; incorporation of quantum effects in the dynamics; and breakdown of the adiabatic approximation, duration of the simulations, and trade-off between accuracy and computational cost of the quantum-mechanical (QM) method employed due to the size of the system, just to mention some. Over the years, groundbreaking developments have appeared in each field. This work does not have the ambition to provide a comprehensive review on each of the three Grand Challenges, which would necessarily require distinct and extensive works (see, e.g., ref (3)). Rather, it aims at highlighting how the three fields are synergistically combined within an effective computational strategy, a virtual spectrometer, able to deliver experimentally accurate transient spectra in silico. We present key recent advances that we believe will have major impact on spectroscopy simulations. A special focus will be devoted to currently pending conceptual bottlenecks, challenges, and opportunities.
The paper is organized as follows: We first give an overview of the state-of-the-art in the above three fields (see Scheme 2) (section 2); then we show some very recent examples for different types of spectroscopy, covering spectral ranges from the near-IR-Vis-UV to the X-ray, and comparing experiments with theoretical predictions for a variety of photochemical and photophysical problems (sections 3.1 and 3.2). Thereby, we highlight the interplay of the three Grand Challenges in the simulations, as well as the approximations involved and the room left for improvements; we proceed showing theoretical proofs-of-concepts for innovative spectroscopic techniques that demonstrate additional information content (section 3.3); we conclude with a critical analysis of the current limitations and future directions of development (section 4).
(where the three Grand Challenges meet ... and fight!)
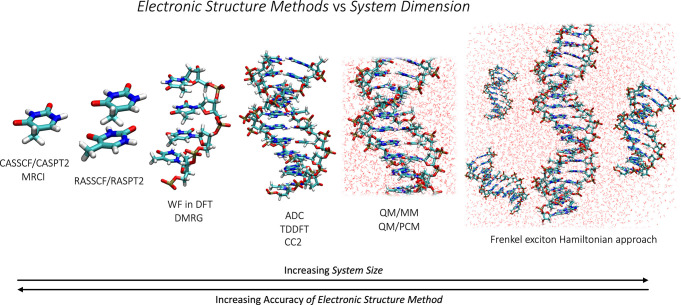
Recent years have witnessed notable progress in electronic structure computational methods, both wavefunction (WF)-based and density functional theory (DFT)-based, which already today permit the fully quantum-mechanical computation of system sizes that were unimaginable a decade ago. Concurrently, hardware architecture developments—increasing CPU and RAM capacities, increasing GPU performance, fast input/output rates on solid-state drives, multi-core and multi-node parallelization techniques—have been exploited to increase speed and efficiency. Notable recent achievements are (i) the implementation of the time-dependent (TD) DFT,4a CC,4b and CASSCF4c,4e protocols on GPUs, which allows calculations with more than 1000 atoms,4e and (ii) the acceleration of the TDDFT4a and CASSCF5a/CASPT25b protocols through massive parallelization, pushing the configuration interaction limit beyond a trillion Slater determinants for CASSCF.5b By exploiting the steadily increasing performance of supercomputing architectures, codes specifically designed to leverage the advantages of GPUs (e.g., Q-Chem,6a Psi4,6b TeraChem6c) and massively parallelized supercomputers (e.g., MPQC,6d NWChem,6e Octupus4a) have appeared.
Beyond profiting from technical hardware innovations, conceptual breakthroughs in WF- and DFT-based theories have been constantly boosting the speed and efficiency, as highlighted in the following subsections correlating specific simulation methods to their appropriate system sizes (see Figure 1).
WF-based multi-reference methods provide by construction an unbiased description of the PES of electronic states of arbitrary nature (covalent, ionic, charge-transfer, singly and doubly excited, etc.). Active-space-based approaches, which are the most prominent representatives of this class of methods, suffer from factorial scaling with active-space size, which until recently restrained their application to small and medium-sized molecules. The implementation of density-fitting and Cholesky decomposition techniques7 for approximating the electron-repulsion integrals, together with more efficient self-consistent field (SCF) solvers,8 makes it possible to handle very large numbers (i.e., thousands) of atomic orbital functions. Novel techniques have emerged recently that solve the configuration interaction problem, one of the major bottlenecks of conventional variational multi-configurational protocols, which currently restricts the active-space size for practical uses to maximally 16 electrons and 16 orbitals. Notable techniques are the density matrix renormalization group (DMRG), which has been applied to CASSCF,9a CASPT2,9b NEVPT2,9c and MRCI;9d the full configuration interaction quantum Monte Carlo (FCIQMC) approach combined with CASSCF;9e the variational two-electron reduced-density-matrix-driven (v2RDM)-CASSCF method;9f the heat-bath configuration interaction (HCI) active-space solver;9g and the adaptive sampling configuration interaction (ASCI) method.9h These implementations make it possible to handle active spaces with many tens of orbitals. An equally effective approach toward mitigating the factorial increase of the full configuration interaction problem is to remove “configurational deadwood”, i.e., configurations which contribute only marginally to the total wavefunction, by introducing a flexible approach to the construction of the active space. Restricted active space (RAS)SCF/RASPT2 and the generalized version GASSCF/GASPT2,10a as well as the closely related ORMAS10b/MRMP210c method, also allow construction of active spaces with a few tens of orbitals.
There are several less costly single-reference WF-based methods for calculating electronic structures,11a such as the hierarchy of algebraic diagrammatic construction (ADC)11b methods (e.g., ADC(2), ADC(3)) and the family of coupled cluster (CC)11c methods (e.g., EOM-CC, LR-CC) that have proven to be reasonably reliable.11d The local variants of these methods, which rely on localized molecular orbitals for the occupied space and pair natural orbitals (PNO), i.e., a compact representation of the virtual space, reduce the scaling of the equations. Recent developments, such as the domain-based local PNO coupled cluster (DLPNO-CC), have reached linear scaling for ground-state problems,11e,11f whereas for excited states the efficient computation of PNOs is a matter of intense research.11d
While single-reference methods generally provide accurate estimates, they often demonstrate weaknesses in the treatment of some states, e.g., of doubly excited character. Another issue, common to all single-reference methods, is their inability to describe the topology of the PES in the vicinity of the conical intersection (CI) between the excited state and the closed-shell ground state.12 The spin-flip family of methods13a offers a rigorous solution to the problem by starting from a high-spin state to generate the lower-spin ground and excited states by single-electron transitions. Recently, these methods have been systematically applied to SR-CI (SF-CIS13b), CC (EOM-SF-CC13c), and ADC (SF-ADC(3)13d), although spin-contamination may impair geometry optimization and molecular dynamics. The issue has been resolved through implementation of the spin-complete spin-flip approach (SC-SF-ORMAS14). Multi-reference flavors of the above-mentioned single-reference WF methods (i.e., MR-CC,15a,15b MR-ADC15c) have been developed but have yet to mature for routine application.16
DFT-based methods for the calculation of excited-state properties combine modest numerical cost and favorable accuracy (since already accounting for correlation energy), thus allowing calculations on larger QM systems as compared to WF-based methods. The linear response TDDFT formulation is nowadays the method of choice for practical applications to excited-state chemistry. However, computational speed comes at the expense of several fundamental shortcomings: (i) transitions with multiple excitations character are not included in TDDFT by definition; (ii) calculations of charge-transfer excitations are particularly challenging due to the inaccurate treatment of long-range correlations;17 and (iii) the traditional TDDFT formulation, similarly to other single-reference methods, fails to describe the topology of the PES in the vicinity of the CI between the excited state and the closed-shell ground state.18 While a solution to (i) is still out of reach,19 long-range corrected functionals20 are showing promising (although not conclusive)17 results with respect to (ii).21a,21b In particular, we note the Minnesota range-separated hybrid meta functionals21c which provide balanced descriptions of valence, Rydberg, and charge-transfer states for both main-group elements and transition metals. The erroneous CI topology problem (iii) is a sign of the more general difficulty of TDDFT in describing strongly correlated systems and has been addressed by many groups. In the following, we briefly outline several approaches which are ready for routine application by non-experts. One such approach is the spin-flip DFT (SF-DFT) and its spin-adapted (spin-complete) version, SA-SF-DFT.22a−22c Another topology-conserving approach is the pseudo-wavefunction (PW) method, which constructs the excited states from a ground-state DFT wavefunction augmented with doubly excited Slater determinants.23a Finally, a new variant of TDDFT, the dual-functional Tamm–Dancoff approximation (DF-TDA), which employs different functionals for orbital optimization and for Hamiltonian construction, has been shown to recover the correct double cone topology in the vicinity of the S1/S0 CI.23b.
The many-body Green’s function GW formalism, originally developed for band structure calculations in solid-state physics,24a,24b has attracted the attention of molecular theoretical chemists as an alternative to DFT thanks to its comparable scaling with system size without the need for empirical parameters. Incorporating the Bethe–Salpeter equation (BSE), which describes the bound states of a two-particle system in a relativistic formalism,24c the BSE/GW approach can be used to compute the bound states of the photoexcited electron and its hole.24b The BSE/GW approach shows some similarities to TDDFT, like the eigenstate representation in terms of single-electron transitions between occupied and virtual molecular orbitals (thus neglecting transitions with multiple-excitations character) and the scaling with system size. However, the underlying formalism relying on perturbational theory is essentially different with respect to TDDFT, which allows for a more accurate description of charge transfer and Rydberg excitations and a mitigated functional dependence.
Substantial efforts have been also recently devoted to combining the advantages of WF and DFT methods.25 Ensemble DFT expresses the density of the system as a weighted average of several Kohn–Sham determinants (i.e., an ensemble state), enabling a multi-configurational DFT treatment.26a The leading method from this family is the spin-restricted ensemble-referenced Kohn–Sham theory (REKS26b), which has been extended to include state-interaction along with state-average optimizations (SI-SA-REKS). WF-in-DFT embedding schemes tackle the problem of strong interaction by separating the two-electron term in a short-range and a long-range contribution, addressed independently at DFT and WF levels, respectively.27a A parameter controls the transition between the two regions, making it essentially a semiempirical approach. Such schemes have been reported for CASSCF, CASPT2, QMC,27b,27c DMRG,27d CC2,27e and ADC.27f Finally, multi-configurational pair DFT (MC-PDFT) extends the original ansatz of Kohn and Sham from a Slater determinant to a multi-configurational wavefunction.28a Recently, MC-PDFT has been combined with DMRG and v2RDM active-space solvers.28b,28c An excellent review of the state-of-the-art in combining WF and DFT methods can be found in ref (29).
Hybrid schemes offer a different perspective to treating large-scale systems, profiting from the localized nature of the electronic excitation. In such cases, a more accurate QM description can be applied to the photoresponsive (reactive) center, while the typically much larger environment, not directly involved in the initial reactive process, is described at a more approximate level.30 If the environment is described using molecular mechanics (MM), the method is known as QM/MM. Schemes such as ONIOM31 provide flexible layer compartmentalization, such as QM(high-level)/QM(low-level)/MM. Conventional QM/MM implementations work in the so-called “electronic embedding” framework, where the environment is represented as a set of point charges that can polarize the QM core. In recent years, next-generation “polarizable embedding” schemes have been established, relying either on inclusion of atom multi-pole moments in addition to the charges or on polarizable point dipoles, treating the mutual polarization of the QM and MM parts self-consistently.32a,32e Further refinement to the basic “electrostatic embedding” scheme, which resolves the electron “spill-out” problem, has been achieved by the polarizable density embedding method, which introduces an intermediate layer between the QM and MM parts represented by its density.33
Hybrid schemes offer an appealing way to extend the scale of the calculation at comparably low cost. Yet, when the photoresponsive center is a multi-chromophore aggregate (e.g., light-harvesting complexes, DNA and RNA strands, porphyrin self-assemblies, etc.), excitations can be strongly delocalized over the monomers and/or inter-chromophore charge-transfer states can be photogenerated, thus forcing the QM region to be enlarged. In such cases, first-principles computation becomes intractable. Collective excitations in systems of coupled chromophores can be treated by the so-called Frenkel–Davydov exciton model.34 In this formalism, the total wavefunction for the collective system is expanded in the basis of monomer excitations (sites), thus requiring only the (trivially parallelizable) computation of the energies of the individual sites and the inter-site couplings, which are conventionally represented via the Coulomb terms only, thus neglecting exchange couplings due to possible overlap of electronic transition densities of close-lying sites. The progress in size scaling of electronic structure methods has facilitated the benchmarking of exciton models with first-principles calculations in small molecular clusters, thus allowing one to study the range of validity of inter-site coupling35 approximations and inspiring research toward models beyond Coulomb coupling. A conceptually appealing (but practically ambiguous) way of obtaining electronic couplings lies in the application of diabatization techniques, as the off-diagonal elements of the diabatic Hamiltonian reflect physical quantities such as the probability for energy or electron transfer.
Various diabatization schemes have been proposed over the years: here we note the 4-fold way,36a,36c the fragment charge difference36d and fragment excitation difference schemes,36e Boys localization adapted to many-body problems,36f,36g and the dipole and quadrupole moments (DQ) scheme.36h Herbert and co-workers proposed an ab initio Frenkel–Davydov exciton model (AIFDEM) that avoids, in principle, any approximations22a by computing explicitly the elements of the full electronic Hamiltonian on the basis of the singly excited Slater determinants. Attempts at incorporating charge-transfer states (not included in the standard Frenkel exciton formulation) have been also recently documented.35b,37a,37b
While exploration of the PES topology requires the availability of energy gradients, non-adiabatic couplings (NACs) are essential for the computation of non-adiabatic dynamics. In WF-based methods, analytical gradients and NACs have recently become available at the XMS-CASPT238a,38b level, thereby paving the way for simulations of mid-size systems at a dynamically correlated level. Regarding the new generation of active-space solver methods, gradients are available for DMRG-CASSCF38c and v2RDM-CASSCF.38d In most single-reference methods, gradients are readily available, yet it has been a long-standing issue how to compute NACs. Formulations within the Tamm–Dancoff approximation scheme36g can be straightforwardly derived for TDDFT,39a ADC2,39b and CC2.39b NACs in the framework of EOM-CC were recently reported.39c The spin-flip version of DFT has also been furnished with NACs,39d while its spin-adapted upgrade is still lacking. A general formulation of NACs between excited states in TDDFT which avoids the Tamm–Dancoff approximation has recently become possible by means of the PW approach.23a,39e From the plethora of mixed WF/DFT methods, gradients have been reported for subsystem DFT,40a frozen-density embedding,15b state-specific MC-PDFT,40b and SI-SA-REKS,40c although only the latter has been also furnished with NACs. Finally, the lack of analytical gradients for excited states represents a current drawback for the BSE/GW method which prevents its widespread application in the field of photochemistry.40d
Molecular dynamics (MD) simulations require solving the time-dependent Schrödinger equation. The Born–Oppenheimer approximation allows one to separate the dynamics of nuclei and electrons, thereby treating the nuclei classically (i.e., applying Newton’s equations of motions) and assuming that the electrons equilibrate instantaneously. The Born–Oppenheimer approximation holds for ground-state conformational changes, a typical example of a near-equilibrium dynamics, but breaks down when the system is promoted to an excited state, in which case approximations have to be made elsewhere (see Figure 2).
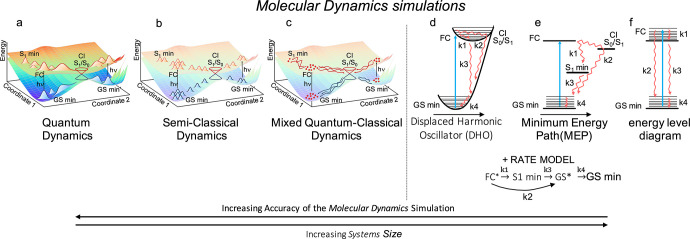
Different levels of sophistication in the description of a photoinduced non-adiabatic process: exact quantum dynamics (a), trajectory-based approaches (b, c), model Hamiltonians (d), and static picture based on reaction paths (e) or energy levels diagrams (f). Details on the range of applicability and limitations about the listed methods can be found in section 2.2. GS: ground state; FC: Franck–Condon state. An extended caption for this figure with additional details can be found in the Supporting Information.
The Schrödinger equation can be solved numerically exactly by representing the Hamiltonian on a grid of time-independent or time-dependent basis functions and propagating their amplitudes, an approach generally labeled as QD (see Figure 2a). The outgoing wave variational principle (OWVP) and R-matrix propagation (RMProp) were originally proposed for treating coupled surfaces in QD.41a More recent advances in the field led to the time-dependent basis approach, the foundation of the multi-configurational time-dependent Hartree (MCTDH),41b which enables a more compact description of the nuclear wavepacket with respect to the time-independent basis and, thus, the simultaneous treatment of several tens of degrees of freedom (DOF).41c,41d A multi-layer variant of the MCTDH, where strongly correlated vibrational DOF are contracted, makes it possible to treat systems with several hundreds of vibrational DOF.41e Research toward full QD simulation for systems with a large number of DOF has become accessible recently by the time-dependent reformulation of the density matrix renormalization group (TD-DMRG).42 Here, only nearest-neighbor interactions are treated explicitly, while the remaining sites are modeled through an effective (i.e., renormalized) basis. This makes TD-DMRG particularly suitable for aggregates dominated by nearest-neighbor interactions. Very recently, surface parametrization methods based on machine learning have been used for improving PESs for QD within a grid-based approach.43
Full-dimensional QD based on an analytical representation of the PES within a harmonic approximation has allowed linear absorption simulations with a remarkable accuracy,41d,41f,41g while analytical models of the CI topology have given invaluable insights into the non-adiabatic dynamics in its vicinity.41h,44a,44b However, the harmonic picture is often incomplete and inadequate for following the evolution of the system away from the Franck–Condon region toward the photoproducts. In such cases, PESs and NACs are computed for reduced dimensionality (up to three or four degrees of freedom) models, considering only modes essential for describing the process of interest.
One limitation of the grid-based approaches is the difficulty in representing the coupling (dynamical in nature) of the photoactive system to its surrounding; for that reason, QD simulations are typically performed in the gas phase. Recent years have witnessed notable progress in incorporating the coupling to the environment, both in a static45a and in a dynamic way,45b,45c the latter allowing cases in which solute and solvent dynamics occur on the same timescale to be treated. Another limitation is that the topology of the involved PES must be known in advance, thus calling for “on-the-fly” methods (see below).
Most current developments in the field of MD are focused on protocols which allow the computation of all necessary ingredients for propagating the system “on the fly”. One such class of protocols models the nuclear wavepacket evolution by means of frozen Gaussians centered at classical trajectories (see Figure 2b). An example is the variational multi-configurational Gaussian wavepacket (vMCG)46 method that is formulated based on MCTDH. The dephasing representation in Gaussian basis (GDR) is conceptually closely related to vMCG, as it also utilizes communicating frozen Gaussian basis functions, yet it is particularly suitable for simulating time-resolved electronic spectra.47a The method comes with a hierarchy of approximations which bridge the exact with the semi-classical picture. The ab initio multiple spawning (AIMS)3d,47b methods consider the Gaussian wavepacket evolving through a swarm of independent trajectories, with bifurcations in regions of strong NAC represented through spawning events. The AIMS formulation, which relates to the GDR under well-defined approximations,47a has itself spawned other approaches, like ab initio multiple cloning (AIMC), which benefits from mean-field (Ehrenfest picture) evolution during periods of strong NAC while simultaneously avoiding mean-field artifacts by flexible expansion of the trajectory basis.48
An intriguing recent development concerns the formulation of semi-classical MD simulation protocols within the framework of the exact factorization (EF) formalism.49a EF proposes a novel form of the wavefunction to solve the time-dependent Schrödinger equation with the direct consequence that nuclei and electrons are propagated by a set of coupled equations of motion which depend on a time-dependent PES. Promising trajectory-based implementations of EF—the coupled-trajectory mixed quantum-classical (CT-MQC)49b scheme which uses TDDFT as the electronic structure method and the decoherence-induced surface hopping based on exact factorization (DISH-XF)49c employing CASSCF/MRCI49c or SI-SA-REKS49d—demonstrate the capability to capture quantum (de)coherence effects. Reference (3d) reviews semi-classical solutions of the time-dependent Schrödinger equation.
In the drastic simplification of modeling the evolving wavepacket through a swarm of independent, non-interacting, classical trajectories, one enters the world of mean-field Ehrenfest and trajectory surface hopping (TSH, see Figure 2c).50 Owing to its simplicity and remarkably good results, considering the level of approximation adopted, the fewest switches formulation of TSH by Tully (i.e., FSSH)50 is nowadays the method of choice for non-adiabatic molecular dynamics simulations, which has been integrated within a vast number of electronic structure methods.3a Nevertheless, the failure of the prototype formulation to describe decoherence, i.e., the gradual collapse of a coherent quantum-mechanical mixture of electronic states into a classical mixture of pure electronic states, properly (over-coherence problem)51a,51c has spawned in recent years a number of modified protocols.3a,3b,51d,51f Furthermore, considerable attention has been devoted to purely practical issues, common to trajectory-based approaches in general. One such issue stems from the steep shape of the NACs in space and the risk of missing them when employing large time steps in the propagation of the nuclei. Norm-preserving interpolation of the time-dependent overlap,52a local diabatization,52b and adaptive time-step protocols52c have been suggested to remedy the issue. An excellent review on trajectory-based non-adiabatic mixed quantum-classical methods is given in ref (3a).
More recently, the FSSH framework has been extended to model Frenkel exciton dynamics in molecular aggregates for studying charge and excitation energy transfer processes by formulating expressions for gradients and coupling terms.3e,53
Despite the progress in electronic structure calculations, the cost associated with the calculation of all the necessary ingredients for performing first-principles MD limits the accessible time window of the “on-the-fly” simulations. An alternative ansatz for describing the dynamics of electronically excited states relies on model Hamiltonians which parametrize the coupling to the bath of vibrational degrees of freedom (both intramolecular and with the environment) by frequency-dependent spectral densities that indicate the strength of the coupling of a given electronic state to the bath. Thereby, the bath is normally assumed to be harmonic and the coupling linear, an approximation known as the displaced harmonic oscillator (DHO) model, which greatly simplifies the problem, as many quantities of interest can be computed analytically.54
In the treatment of multi-chromophoric systems with parametrized Hamiltonians, the system–bath coupling is still handled within the DHO framework. The Hamiltonian contains an additional coupling term, the inter-chromophore coupling. Depending on its strength, the aggregate can be modeled either in a localized (site) basis (“weak” coupling regime) or in a delocalized (exciton) basis (“strong” coupling regime).3f Different theories describe energy and/or electron-transfer dynamics in these contrasting regimes: as incoherent hops between sites in the Förster model,55a,55b which treats the inter-chromophore couplings perturbatively, and as relaxation between exciton states in the Redfield theory,56a,55b which instead treats the coupling to the bath perturbatively. Modifications of both formulations (e.g., the generalized Foerster55c and modified Redfield56b−56d theories) aim at expanding their application range.
A number of methods have been developed that go beyond the above-mentioned perturbative treatments (still within the DHO framework). Methods like the hierarchical equations of motion (HEOM),57a the iterative quasi-adiabatic propagator path integral (i-QUAPI),57b and the partially linearized density matrix (PLDM) dynamics57c are considered superior. However, they become computationally much more demanding and therefore limited to specific forms of the spectral density. Implementations to massively parallelized supercomputer architectures, GPU-acceleration, as well as tractable approximations are required for their practical applications.57d−57g
Most ultrafast optical spectroscopy experiments detect the time-dependent third-order non-linear optical response of the system under study. In a general realization, a first actinic light pulse sequence (the “pump”) perturbs the electronic density of the system, initiating its dynamics. After a delay, another sequence of pulses (the “probe”) is used to create a non-linear polarization in the system emitting a field, the response, which is recorded by the detector (see Figure 3). Such light–matter interactions are the object of Theoretical Spectroscopy, whose aim is to identify spectroscopic observables, to elaborate the mathematical framework for their simulation, and to relate the line shapes and evolution of the spectral features to the underlying molecular processes. Theoretical spectroscopy also allows designing tailored pulse sequences aimed at highlighting novel observables, increasing signal-to-noise ratio, and suppressing undesired background signals, profiting from the tunability of pulse parameters (such as duration, central frequency, bandwidth, and polarization) while respecting technical constraints in the preparation of the pulses.
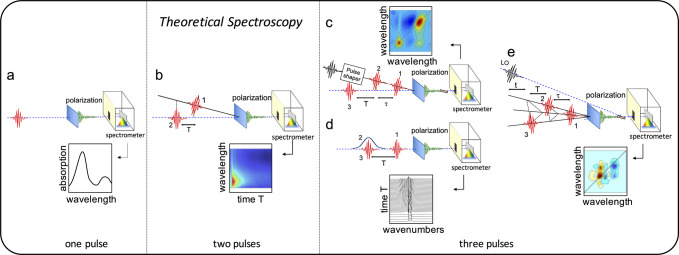
Experimental set-ups for linear and non-linear optical spectroscopy: (a) one-pulse (linear), (b) two-pulse (pump–probe), and (c–e) three-pulse (two-dimensional) spectroscopy. Examples of recent simulations of pump–probe, two-dimensional, and time-resolved Raman spectroscopy are provided in sections 3.1, 3.2 and 3.3, respectively. LO: local oscillator. An extended caption for this figure with additional details can be found in the Supporting Information.
In the most general representation, the nth order polarization (with respect to the external driving field) induced in the system by the sequence of electric fields can be treated non-perturbatively by incorporating the fields into the system’s Hamiltonian. This method permits the exact numerical simulation of the dynamics of the driven system for fields of arbitrary strength and duration.58 The non-perturbative approach makes it possible to study, without any approximation, the effects of pulse parameters like central frequency, bandwidth, etc., including strong laser fields and temporally overlapping pulses.
More often the field–matter interaction is treated in the perturbative (i.e., weak field) regime, which is the topic of this Perspective. The nth order term of the polarization is expressed as the sum of n-dimensional time integrals over non-linear response functions given in terms of quantum-mechanical dipole correlation functions. Within the perturbative treatment, pulses are commonly assumed to be temporally non-overlapping and described by Dirac delta functions, i.e., short compared to the investigated dynamics, which simplifies drastically the calculations. Another advantage of the perturbative treatment is that different response functions can be computed separately, providing a convenient theoretical framework for their classification.54,59,60
In principle, the master equations derived from the perturbative and non-perturbative treatment can be solved exactly quantum-mechanically, given the knowledge of the system Hamiltonian. The bottleneck of this fully quantum-mechanical wavepacket propagation is the high cost of pre-computing the PES, which limits its use to simple models, such as di- and triatomics, as well as some elementary chromophores (ethylene, formaldehyde, pyrazine).41d,61
A more convenient approach for solving the equations involves the semi-classical stochastic modeling of bath fluctuations. Thereby, the response function is calculated by averaging over an ensemble of realizations, propagated through the trajectory-based MD approaches described in the previous section (sub-sections 2.2.2 and 2.2.3). Apart from the considerable computational cost associated with the propagation of a swarm of trajectories, semi-classical methods must confront the issue of defining the density matrix and treating the quantum feedback on the classical bath during a coherence state evolution, a problem particularly severe in surface hopping formulations.51b,62 Trajectory-based implementations of linear absorption,63a transient absorption and emission, photoionization spectroscopy,47a,63b,63c stimulated Raman,63d−63f and two-dimensional electronic spectroscopy (2DES)63g−63i that address these issues to various levels of sophistication have been documented. Due to the high cost associated with the more accurate description of coherences, most simulations adopt the semi-classical Franck–Condon (also called “snapshot”) approximation, neglecting the time-dependence of the observable of interest during the coherence evolution, an approximation strictly valid only when the value of the observable fluctuates slowly with respect to nuclear relaxation.63g,64a,64b Due to its limitations, the snapshot approximation is more useful for resolving spectral features of ground-state conformational dynamics64c,64d and long-living excited states.64d,64e
The linear and non-linear optical responses can be modeled analytically for Hamiltonians constructed within the harmonic approximation (DHO model, see section 2.2.4) relying on the cumulant expansion of Gaussian fluctuations (CGF) to second order.54 The spectrum is computed as a sum over all states (SOS), each one characterized by its energy, oscillator strength, and spectral density, which give rise to the signal’s position, intensity, and line shape, respectively (see Figure 4 for a demonstration of the influence of the different approximations on the simulation of the signal line shapes). The CGF formulation is exact for adiabatic dynamics, while non-adiabatic effects can be included at various levels of sophistication.65a Generalizations beyond the harmonic approximation65b and weak system–bath coupling have also been reported recently.65c
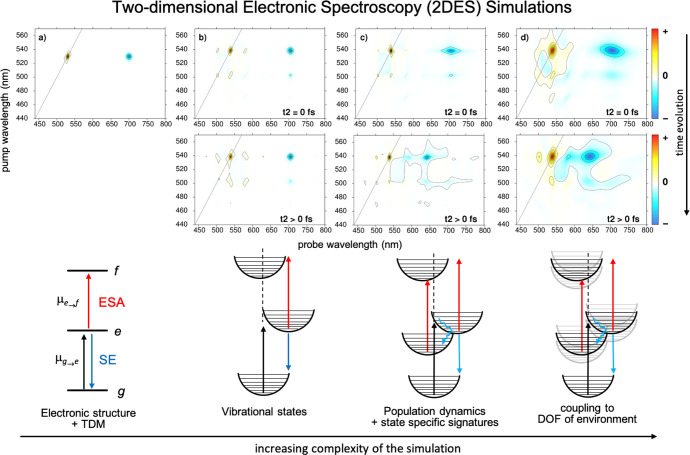
Various flavors of increasing accuracy in the simulation of two-dimensional electronic spectroscopy (2DES): (a) stick spectrum, (b) plus coupling of the electronic and intramolecular vibrational degrees of freedom, (c) plus electronic population dynamics, (d) plus coupling of the continuum of degrees of freedom of the environment. SE: stimulated emission; ESA: excited-state absorption. An extended caption for this figure with additional details can be found in the Supporting Information.
For strongly coupled aggregates (Frenkel–Davydov exciton model, see section 2.1.7), the SOS approach quickly becomes too expensive as the number of excited states grows quadratically with the system size. To circumvent this, a quasi-particle formulation of the CGF method has been developed which scales more favorably with system size.60,66 Yet, it exhibits some limitations considering the treatment of non-adiabatic effects.
Until recently, the practical application of the above theories relied on empirical parameters obtained experimentally or on the basis of simplified molecular models. The past few years have witnessed a shift toward a fully computational estimate of the required ingredients: couplings to discrete intramolecular vibrational degrees of freedom via projection methods,67a−67c couplings to the continuum of solvent vibrational degrees of freedom from MD simulations,34,57c and electronic structure of fundamental chromophores with state-of-the-art QM methods.3i
Besides the level of precision of the underlying MD, another bottleneck in the simulation of time-resolved electronic spectroscopy is the cost associated with the computation of the measured physical quantities: normal-mode frequencies, excited-state absorptions and transition dipole moments in the visible and ultraviolet, ionic-state energies in photoelectron spectroscopy, core–valence transitions in resonant inelastic X-ray scattering, transition densities in X-ray diffraction, and electronic polarizabilities in attosecond Raman spectroscopy. Recent years have witnessed tremendous progress in the development of protocols for monitoring these quantities along the dynamics simulation. Protocols for computing the optical response of excited states in conjugated polyenes and aromatic compounds were developed within the framework of multi-configurational wavefunction theory.68 The multi-configurational nature of excited states is notoriously a problem for DFT. A recent method for computing excited-state absorptions combines real-time (RT) and linear-response (LR) TDDFT.69 Another approach computes Dyson norms between neutral and ionic states within multi-configurational wavefunction theory, as required for obtaining signal intensities in photoelectron spectroscopy70 (section 3.1). A simple but elegant projection technique, in combination with RASSCF theory, has made accessible single and multiple core–valence transition energies and dipole moments.71
(where, after fighting, the three Grand Challenges cooperate)
In the previous section, we reviewed the most recent developments in the fields of electronic structure theory, molecular dynamics simulations, and theoretical spectroscopy. In this section, we demonstrate, based on selected examples, how these fields are forced to cooperate to produce from first principles time-dependent molecular spectra which can be directly compared to the experimental results. In the first two subsections, we show a one-to-one comparison between theory and experiment for non-linear two-pulse (i.e., pump–probe, section 3.1) and three-pulse (i.e., two-dimensional, section 3.2) spectroscopy (see Figure 3). The reported examples set the current state-of-the-art and the frontier between “explored” and “unexplored” territories, as shown in Figure 5. Therefore, when discussing these cases, ongoing challenges and directions for future improvements are highlighted. In section 3.3, we demonstrate the capabilities of theory to envision novel spectroscopic techniques, whose benefits will likely trigger future experiments.
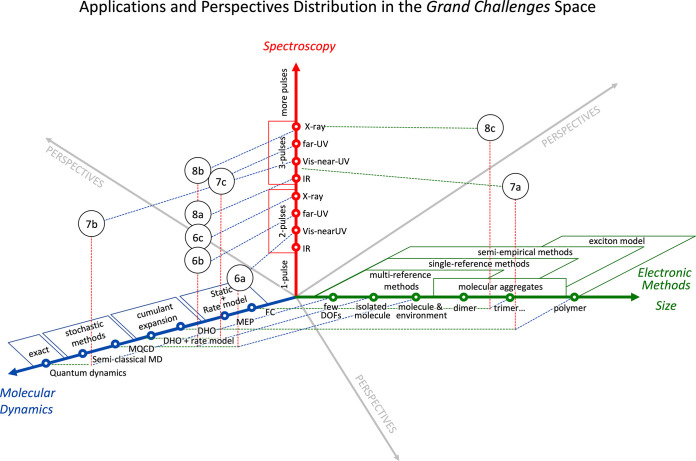
Schematic representation of the three Grand Challenges: choosing a suitable electronic structure method to handle the dimensionality of the system (green axis), describing the non-adiabatic molecular dynamics (blue arrow), and implementing protocols for various types of non-linear spectroscopy (red arrow). Circles with labels refer to examples discussed in section 3 and shown in Figures 6, 7, and 8.
Pump–probe spectroscopy (see Figure 3b), also known as transient absorption (TA), is a widespread technique for studying MD thanks to its straightforward experimental realization and the ease to interpret the spectra. Over the years, simulations have evolved to a level where TA spectra of small and medium-size chromophores (up to 20–30 atoms) can already be computed very accurately from first principles, thereby revealing the physical phenomena behind the spectroscopic signatures. Below, the state-of-the-art is illustrated by three very recent examples.
Broadband (Vis-UV) TA spectroscopy simulations were combined with hybrid QM/MM mixed quantum-classical trajectory-based non-adiabatic dynamics to study the ultrafast excited-state dynamics of the sulfur substituted nucleobase 4-thiouracil in water (Figure 6a).67a,72 Electronic structure calculations were done at the multi-configurational second order perturbation (CASPT2) level of theory. The results explain the reason for the experimental mismatch between the timescales for the decay of the stimulated emission (SE) from the bright ππ* state (76 fs) and the rise of the excited-state absorption (ESA) of the triplet state (225 fs). The work provides compelling evidence that the intersystem crossing occurs via an intermediate dark state of nπ* nature previously reported in gas-phase studies.73 Transient spectra within the CGF method parametrized on the basis of the simulated dynamics reproduce all characteristic spectral features, such as the origin of the ESA and the intensity beats in the SE.
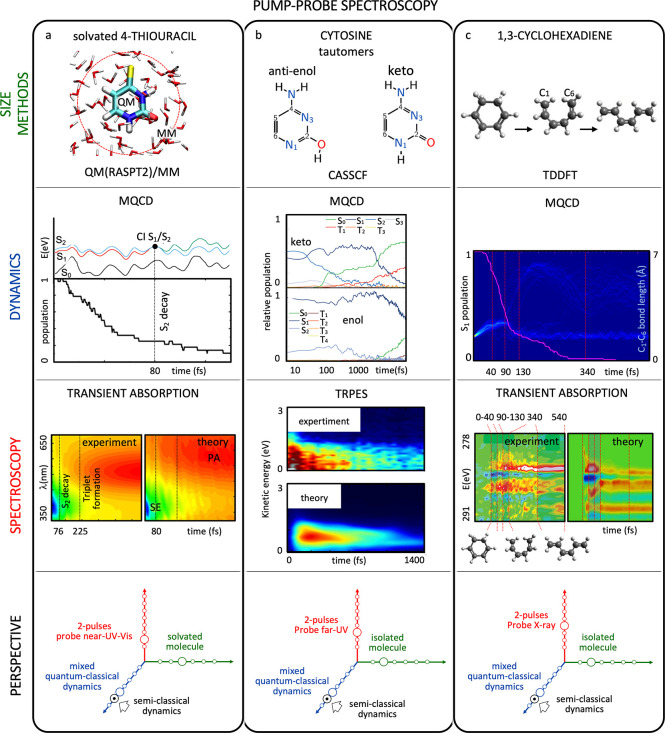
Three examples of pump–probe spectroscopy simulations from first principles and comparison to experiments: (a) solvated thiouracil (ref (67a)), (b) isolated cytosine (ref (74)), and (c) isolated cyclohexadiene (ref (76)). The state-of-the-art of the simulation in terms of system size/electronic structure method, molecular dynamics protocol, and spectroscopy technique are shown in the schematic representation of the three Grand Challenges (see Figure 5). Advancements in the simulations that would improve the agreement with the experiment are indicated with a black arrow. An extended caption for this figure with additional details can be found in the Supporting Information. Figure rights: (a) Adapted with permission from ref (67a). Copyright 2018 American Chemical Society. (b) Adapted with permission from ref (74a). Licensed under CC BY 4.0. Copyright 2016 Springer Nature. Reprinted in part with permission from ref (74b). Copyright 2013 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. (c) Adapted with permission from ref (76). Copyright 2017 American Association for the Advancement of Science.
Time-resolved photoelectron spectroscopy (TRPES) simulations were performed on the keto and enol tautomers of cytosine (Figure 6b).74 Theoretical spectra adopting the snapshot approximation were obtained by computing the Dyson norms between the singlet/triplet states of the neutral and the doublet/quartet states of the ionized species along gas-phase trajectory-based dynamics on the neutral species within TSSH framework, explicitly considering intersystem crossing events. Electronic structure calculations were carried out at CASSCF level of theory. The photoexcited bright ππ* state initially relaxes to the singlet nπ* state, from which it bifurcates into channels which either explore the CI seam with the ground state or lead to the population of a triplet state. The two tautomers are found to decay through different regions of the seam. These competing processes occur on similar timescales, so that the different relaxation pathways are completely obscured in the total photoionization signal. This calls for the design of new experimental setups capable of discriminating the individual channels.
The light-activated electrocyclic ring-opening process of 1,3-cyclohexadiene represents a prototypical photochemical pericyclic reaction mediated by a CI.75 Soft X-ray spectroscopy simulations on top of non-adiabatic mixed quantum-classical molecular dynamics were able to reproduce the experimentally observed spectroscopic signature near the carbon K-edge (∼284 eV), a fingerprint of the population of the intermediate pericyclic minimum (Figure 6c).76 TDDFT was employed to simulate core–valence transitions along the trajectories. The simulations reproduced the timescale of the electronic rearrangement required to initiate the pericyclic reaction (∼60 fs), as well as the lifetime of the excited state (∼110 fs).
The above-mentioned examples, covering a broad spectral interval from the visible to the soft X-ray, show a striking agreement between theory and simulation. Such agreement is remarkable in light of the numerous involved approximations. For the future we expect applications to implement advanced semi-classical dynamics simulation protocols beyond the Tully approximation (such as AIMS3d or the emerging schemes based on the exact factorization (EF)49a). A rigorous comparison between various approximations of the non-adiabatic dynamics would allow a better understanding of the range of their validity. Furthermore, we expect computational software to implement the many new tools for easily simulating various TA signal features, thus rendering spectroscopy simulations routinely accessible also to non-experts. This would allow researchers to predict spectral fingerprints of the photoinduced processes and to obtain in silico the optimal pulse parameters (such as wavelength, duration, polarization, etc.) required for their detection in real experiments.
Two-dimensional (2D) spectroscopy employs a sequence of properly timed and phase-locked pulses to fully resolve the field emitted by the third-order non-linear polarization of the system (see Figure 3c,e). Using a Fourier transform approach, 2D spectroscopy makes it possible to correlate spectral signatures to the pump and probe frequencies in a 2D plot, thus increasing the spectral resolution without sacrificing temporal resolution. 2D spectroscopy is particularly appealing for the study of multi-chromophoric systems with highly congested spectra which are difficult to interpret with the conventional TA techniques. With respect to its one-dimensional counterpart, 2D spectroscopy makes it possible to (a) identify chromophore-specific signatures and inter-chromophore couplings, (b) monitor energy and charge transfer processes between coupled states/chromophores, and (c) measure separately homogeneous and inhomogeneous contribution to the linewidth of optical transitions and follow their temporal evolution. 2D spectroscopy is nowadays established in the infrared (two-dimensional infrared spectroscopy, 2DIR) and in the visible (2D two-dimensional electronic spectroscopy, 2DES) with applications in solvation dynamics, conformational analysis, protein folding and unfolding, and energy and charge transfer.77 The required interferometric stability between pulses makes the practical realization of 2DES techniques at shorter wavelengths (UV and beyond) considerably more difficult.3h The interpretation of the 2D spectra brings challenges of its own, like the assignment of spectral beats to either electronic coherences or molecular vibrations.78a−78e Thus, much of the theoretical effort has been focused on understanding the origin of the signals and the line shapes on simple models. Overall, due to the intricacy of realization and interpretation, only a few works have reported a face-to-face comparison between experiment and simulation. Below, the state-of-the-art is illustrated by three recent examples:
Simulations of broadband (near-IR-Vis) 2DES on the light-harvesting complex 2 (LH2) of a purple bacterium integrated quantum chemistry and an electron–phonon exciton model (see Figure 7a).79 Electronic structure calculations were executed at both the single- (TDDFT) and multi-reference (CASPT2) levels in combination with state-of-the-art models for treating the environment (atomistic and polarizable embeddings). Bath dynamics and exciton transport between the pigments were described by Redfield (strong coupling regime) and Förster (weak coupling regime) theories. The work provides an interpretation of the main features of the 2DES spectrum at very short times.80 In particular, the characteristic energy splitting of the bacteriochlorophyll bands and the vibrational progression in the carotenoid region reinforced the hypothesis of the involvement of a dark intermediate state of the carotenoid in the energy-transfer process.
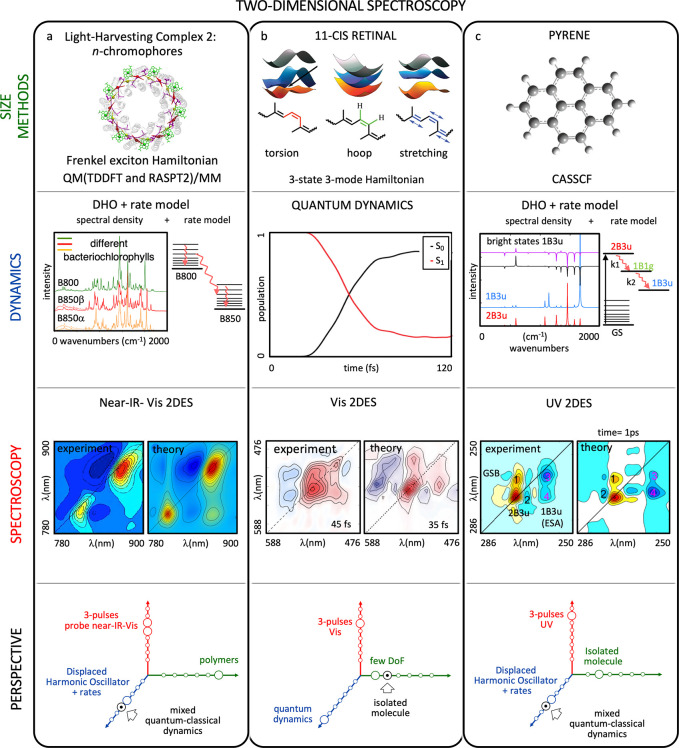
Three examples of two-dimensional electronic spectroscopy (2DES) simulations from first principles and comparison to experiments: (a) light-harvesting complex 2 (ref (79)), (b) retinal protonated Schiff base (refs (81) and (82)), and (c) pyrene (ref (67c)). The state-of-the-art of the simulation in terms of system size/electronic structure method, molecular dynamics protocol, and spectroscopy technique are shown in the schematic representation of the three Grand Challenges (see Figure 5). Advancements in the simulations that would improve the agreement with the experiment are indicated with a black arrow. An extended caption for this figure with additional details can be found in the Supporting Information. Figure rights: (a) Adapted with permission from ref (79). Copyright 2017 American Chemical Society. (b) Adapted by permission of the Royal Society of Chemistry from ref (81). Experimental spectrum adapted with permission from ref (82). Copyright 2017 American Chemical Society. (c) Adapted with permission from ref (67c).
Theoretical 2DES was used to study the photoisomerization of the 11-cis isomer of the retinal chromophore inside the protein rhodopsin (see Figure 7b).81 Thereby, the researchers relied on a parametrized three-mode three-state model Hamiltonian which explicitly considers the hydrogen out-of-plane (HOOP) mode besides the torsional and ethylene stretch coordinates, as well as an additional excited state giving rise to ESA in the targeted spectral window. 2DES simulations adopting the perturbative regime on top of exact time-dependent wavepacket propagation conducted with the model Hamiltonian agree reasonably well with experiment and demonstrate that the origin of the observed absorptive spectral features is not the HOOP mode as was previously suggested.81 Instead, it was found that an ESA to a higher lying state which is not involved in the isomerization “contaminates” the spectra at early times.
2DES simulations mapped the spectral signatures of the ultrafast excited-state deactivation of pyrene, promoted in its second bright state absorbing in the UV (see Figure 7c).67c The simulations were conducted with the CGF parametrized by electronic structure calculations at the multi-configurational second-order perturbation (CASPT2) level. The simulations resolve the nature of the high-frequency vibrations which give rise to a checkerboard pattern in the experimental spectra,67c assigning them to carbon–carbon stretchings. Furthermore, a low-frequency quantum beat arising from an excited-state wavepacket83 was matched to an in-plane bending vibration activated upon crossing a CI. The agreement with the experiments3h demonstrates that wavefunction-based techniques are capable of accurately reproducing the high-energy manifold of organic chromophores.
The presented 2DES simulations show a good agreement with the experimental data, but they have not yet matured to the level of TA simulations. The spectra lack occasionally relevant features (e.g., ESA peaks), and the modeling of the signal line shape is less satisfactory owing to the drastic approximations unavoidable to tackle the increased system complexity. For the future we expect applications to consider in a rigorous way transitions to higher lying states, giving rise to significant ESA contributions.67c,79,81 Furthermore, we expect applications to employ advanced dynamics simulation protocols to describe exciton energy and charge transport, as well as relaxation pathways that go beyond the Redfield and CGF approximations. This undertaking seems more and more feasible with the recent extension of the FSSH framework to exciton dynamics3e,53 and trajectory-based 2DES simulation protocols.63g−63i
With the advances in computational technologies and the developments in theoretical and experimental ultrafast spectroscopy, the synergy between experiment and theory is steadily increasingly. On the one side, simulations are not plagued by the technical limitations accompanying the experiments (e.g., limited pulse bandwidth, low phase stability, low signal-to-noise ratio, solvent artifacts, etc.). Complex pulse sequences can be conceived to resolve fingerprints of the process under investigation, thus inspiring experimentalists to search for ways to overcome the restrictions. For instance, three-pulse femtosecond and attosecond stimulated Raman spectroscopy techniques have been recently proposed. Very remarkably, off-resonant attosecond stimulated Raman spectroscopy, also known as transient redistribution of ultrafast electronic coherences in attosecond Raman signals (TRUECARS), holds the promise to have the necessary temporal resolution and the sensitivity to resolve the passage of a wavepacket through a CI.84 On the other hand, experimental breakthroughs (e.g., the X-ray free electron laser) allow scientists to explore previously inaccessible spectral regions and to resolve novel phenomena, thus stimulating theoretical efforts in rationalizing the observations and in conceiving novel techniques that exploit the new laser sources. For instance, recent advances in X-ray laser technology reporting bright and ultrashort pulses85a−85c have sprung a number of non-linear techniques exploiting the broad bandwidth, short duration, spatial localization of the excitation, and element specificity of exahertz pulses.3g,3j Among these techniques we note (a) X-ray TA spectroscopy, the counterpart of optical TA spectroscopy,86a−86c which has already been successfully implemented experimentally;76,87 (b) 2D coherent X-ray spectroscopy,86d−86f which extends the benefits of 2DES to this frequency range; and (c) time-resolved X-ray diffraction, which allows us to resolve MD in time and space.86g−86j
In the following, we present three examples which illustrate some of these novel techniques.
(88) FSRS is a three-pulse experiment in which the dynamics of a molecule is initiated by an actinic pulse and the evolution of the vibrational spectrum is probed by stimulated Raman scattering (SRS), with a Raman sequence consisting of a picosecond Raman pump synchronized with a femtosecond Stokes pulse. In a first application, a simulation protocol was reported that combined non-adiabatic on-the-fly MD at the CASSCF level of theory with a mode-tracking algorithm to obtain the instantaneous frequencies of high-frequency spectator modes (C–H and N–H stretching) of photoexcited uracil (see Figure 8a)63e and demonstrated that the FSRS signal is sensitive to the non-adiabatic relaxation events in the vicinity of CIs. The experimental implementation of this technique could help determine the relative importance of the ππ* → ground state and the ππ* → nπ* deactivation channels in DNA/RNA, still a matter of intense debate.
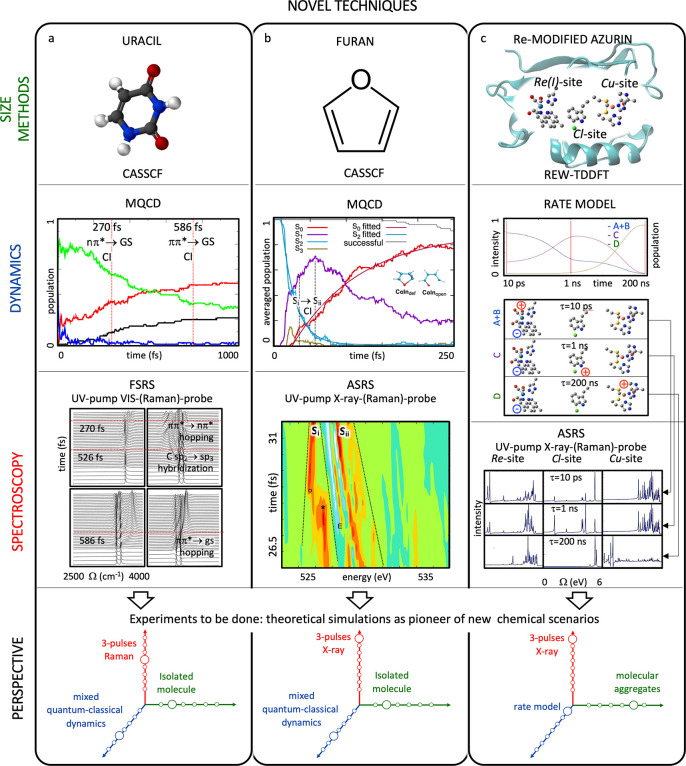
Three examples of novel spectroscopy simulation protocols of time-resolved vibrational and electronic Raman signal applied to (a) uracil (ref (63e)), (b) furan (ref (89)), and (c) azurin (ref (90)). The state-of-the-art of the simulation in terms of system size/electronic structure method, molecular dynamics protocol, and spectroscopy technique are shown in the schematic representation of the three Grand Challenges (see Figure 5). An extended caption for this figure with additional details can be found in the Supporting Information. Figures rights: (a) Adapted with permission from ref (63e). Copyright 2014 ACS. (b) Adapted from ref (89), licensed under a Creative Commons Attribution (CC BY) license. (c) Adapted with permission from ref (90).
ASRS extends the ideas of FSRS to the attosecond time domain by superimposing a femtosecond Raman pump pulse with an attosecond Stokes pulse. The ASRS signals are highly sensitive to electronic coherences either created by the inelastic Raman process (resonant with core–valence transitions) induced by the hybrid broad-narrow pulse sequence or emerging from the off-diagonal elements of the density matrix which become different from zero in the case of non-adiabatic events such as the passage through or close to a CI. As the temporal and spectral resolution of the proposed experiment are not Fourier-conjugate pairs, this setup can monitor the evolution of the coherences with an attosecond temporal resolution without sacrificing spectral resolution.
The ability of ASRS to monitor the few femtoseconds short passage through a CI has been theoretically demonstrated on the ring-opening of furan (see Figure 8b).89 ASRS signals were simulated by on-the-fly MD at the CASSCF level in combination with oxygen core–valence calculations at the RASSCF level.
ASRS tracks coherences between valence states and is, therefore, particularly sensitive to variation of the electronic structure with the oxidation state. By probing valence dynamics via a core-excited intermediate, ASRS combines the spatial selectivity of X-ray spectroscopy with the much narrower linewidths of visible and UV spectra. ASRS in azurin was proposed for resolving long-range electron transfer, a central step in many biological redox reactions in living organisms (see Figure 8c).90 Using a simple kinetic model fitted to experimental lifetimes and coupled to restricted excitation window time-dependent density functional theory (REW-TDDFT)91 with the LC-PBE0 functional and conductor-like implicit solvent model (COSMO) to represent solvent effects, the authors demonstrated the higher sensitivity of ASRS in comparison to transient X-ray absorption spectroscopy.
(... and revolutions)
The past decade has witnessed remarkable progress in modeling transient spectroscopic signals of photoinduced events for large-size photoactive molecular systems in realistic conditions. This Perspective shows that computational spectroscopy has grown to its full maturity, going much beyond being a nice, but ancillary, complement of experiments. In many cases, it holds experimental accuracy, becoming a mandatory tool for the interpretation of complex multi-pulse spectroscopies. In other cases, simulations precede experimental capabilities and become drivers for future experimental developments.
Despite the many successes, there are still several outstanding problems within the three Grand Challenges, both theoretical and conceptual, which we briefly outline in this concluding section.
A great effort will be needed in assessing the performance and understanding the advantages and limitations of the different methods by benchmarking them against established approaches (we refer to ref (92a) for a nice essay on the subject).21a,92b−92g This will require new codes and software interfaces (e.g., see SHARC,93a COBRAMM,93b NEWTON-X93c) that allow various QM methods to be run on the same footing.
We have shown (see Figure 7a) that the Frenkel exciton Hamiltonian is a convenient approach to model large and complex multi-chromophore systems and simulate their non-linear spectroscopy. However, this is based on the assumption that electronic excitations are (semi)localized on weakly interacting chromophores. Strongly interacting (and, possibly, reacting) units, displaying qualitatively different (possibly crossing), highly anharmonic ground- and excited-state PESs (as for instance DNA/RNA oligomers94), are still challenging to describe. A promising strategy is to marry the brute-force approach of increasing the size of the QM region to the excitonic one by the use of larger, but still computationally manageable, QM building blocks for the exciton Hamiltonian, which embrace a set of strongly interacting chromophores. This would make it possible to describe the photoinduced processes (including delocalized and charge-transfer states), still concurrently accounting for the interactions among the selected QM regions as described by the exciton Hamiltonian and thus leveraging the intrinsic parallelizability of the calculations of its terms that is suitable for modern multi-core architectures and GPU accelerated algorithms.
Deeply integrated QM and ML methods are expected to disclose new practical approximate ways to speed up electronic structure calculations. For instance, ML could help in avoiding the explicit estimate of the many expensive, but negligible, bottleneck terms in multi-configurational and perturbative QM methods, still retaining their accuracy. Development and benchmarking of these approaches will be needed to prove their robustness and general applicability (see ref (95)).
Driven by the main computing market leaders as well as new players (e.g., IBM, Google, Microsoft, D-Wave, etc.), the quest for quantum supremacy has already led to prototype CPUs based on different and competing quantum bit architectures. This makes the idea of modeling a quantum system by a quantum computer more than a dream (e.g., refs (96a−96c)). Notably, first applications and software packages for quantum computing simulations have just appeared (e.g., OpenFermion),97 with IBM already opening its quantum computing platform to the scientific community, thus making this one of the most attractive directions for the future.
The strength of the exciton Hamiltonian approach is that it can be coupled to a TSH non-adiabatic dynamics scheme, such as the Tully’s FSSH. This requires updating the parameters of the electronic Hamiltonian on-the-fly, as the nuclear configuration evolves in time, by computing at each step the derivatives of the exciton model parameters with respect to the nuclear coordinates, and mapping these and the NACs.3f In aggregates, due to the many close-lying excited states, new problems arise as one needs to either compute many NACs at each step of the propagation (strongly coupled chromophores) or deal with trivial crossings (non-interacting chromophores in the aggregate). This is a very promising strategy, as recently shown by a few preliminary works.3e,53 The study of the photophysics of DNA/RNA (a test case for flexible strongly coupled and reacting multi-chromophoric systems) will provide an excellent playground for these developments.
Developments of atomistic ML tools, based on transfer learning on gold standard datasets optimally spanning the physics of interest, promise to deliver with low computational cost PESs as accurate as those obtained from the most expensive QM methods. ML approaches can also be used to produce, by a trained and driven re-parametrization of classical FFs, low-cost and accurate analytical PESs for the excited states, thus allowing non-adiabatic MD to be performed at the cost of classical MD. Recent results and proofs of concept are very promising.98a−98c An alternative technique for obtaining coupled high-dimensional PESs is the anchor points reactive potential (APRP) method, which describes few large-amplitude (reactive) modes explicitly based on QM calculations, whereas small-amplitude (secondary) modes are described in MM-like terms.36c,98d Overall, these methods are expected to speed up MD and improve the accuracy by delivering optimal PESs.
Future developments in theoretical spectroscopy are intimately linked to the corresponding advances in experimental techniques, enabled by either novel light sources (such as ultrashort coherent X-rays) or novel methodologies (such as ultrafast spectroscopy with quantum light).
Multi-dimensional extensions of some of the presented novel techniques (e.g., 2D-FSRS)99 would provide access to anharmonicities and inter-mode couplings in excited states that are influenced by the coupling in the vicinity of a CI.3g
Time-resolved diffraction with ultrashort X-ray or electron pulses has the advantage to directly encode spatial information, revealing the location of the created coherences:3g data interpretation will need accurate modeling of these signals.100
Simplified tools need to be made available to experimentalists and non-expert users to assist spectroscopic characterization of molecular materials beyond the academic lab. The development of black-box tools for spectral analysis and interpretation, and their integration within a productive environment, would be a major achievement, calling for a standardization of the language through the development of a common ontology in materials modeling.101
In summary, to achieve a complete and accurate description of the complex transient spectroscopy in large size chromophores and multi-chromophoric systems, major challenges are still in the way. Nonetheless, the smart integration of classical and quantum chemical (static and dynamic) approaches and the improvements in exciton Hamiltonian schemes, combined with the development in high-performance multi-core architectures, GPU accelerated algorithms, and machine learning techniques, draw a clear and promising path. Finally, the emerging field of quantum computing with the first example of quantum supremacy just appeared,102 which seems to announce the dawn of a new era, painting an even more optimistic horizon. This revolution will likely lead to a disruptive change in the high-performance computing world as we know it, heralding a plot twist in Quantum Chemistry Tales.
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c04952.
Extended versions of the figure captions and related references (PDF)
The authors declare no competing financial interest.
The authors acknowledge support from the H2020-NMBP-TO-IND-2018-2020/DT-NMBP-09-2018 project SIMDOME, Grant agreement No. 814492. M.G. and G.C. acknowledge support from the European Research Council Advanced Grant STRATUS (ERC2011AdG No. 291198). Financial support from the PHANTOMS project, PRIN: PROGETTI DI RICERCA DI RILEVANTE INTERESSE NAZIONALE – Bando 2017, Prot. 2017A4XRCA, is acknowledged. G.C. acknowledges support from the PRIN 2017 project 201795SBA3 – HARVEST. We thank Francesco Segatta for the useful discussions.
| 2D | two-dimensional |
| 2DES | two-dimensional electronic spectroscopy |
| 2DIR | two-dimensional infrared |
| ADC | algebraic diagrammatic construction |
| AIFDEM | ab initio Frenkel–Davydov exciton model |
| AIMC | ab initio multiple cloning |
| AIMS | ab initio multiple spawning |
| APRP | anchor points reactive potential |
| ASCI | adaptive sampling configuration interaction |
| ASRS | attosecond stimulated Raman scattering |
| CASSCF | complete active space self-consistent field |
| CASPT2 | complete active space second-order perturbation theory |
| CC | coupled cluster |
| CC2 | coupled-cluster singles and doubles |
| CGF | cumulant expansion of Gaussian fluctuations |
| CI | conical intersection |
| CIS | configuration interaction singles |
| COSMO | conductor-like screening model |
| CT-MQC | coupled-trajectory mixed quantum-classical |
| DFT | density functional theory |
| DHO | displaced harmonic oscillator |
| DISH-XF | decoherence-induced surface hopping based on exact factorization |
| DMRG | density matrix renormalization group |
| DOF | degrees of freedom |
| DQ | dipole and quadrupole moments |
| EF | exact factorization formalism |
| EMMO | European materials modeling ontology release |
| EOM-CC | equation-of-motion coupled cluster |
| EOM-SF-CC | equation-of-motion spin-flip coupled cluster |
| ESA | excited-state absorption |
| FCIQMC | full configuration interaction quantum Monte Carlo |
| FF | force field |
| FSRS | femtosecond stimulated Raman scattering |
| FSSH | fewest switches surface hopping |
| GDR | dephasing representation in Gaussian basis |
| GASPT2 | generalized active space second-order perturbation theory |
| GASSCF | generalized active space self-consistent field |
| GPU | graphic processing unit for data-parallel computing |
| HCI | heat-bath configuration interaction |
| HEOM | hierarchical equations of motion |
| HOOP | hydrogen out-of-plane |
| i-QUAPI | iterative quasi-adiabatic propagator path integral |
| LH2 | light-harvesting complex 2 |
| LR | linear response |
| LR-CC | linear-response coupled cluster |
| MC | Monte Carlo |
| MC-PDFT | multi-configurational pair density functional theory |
| MCTDH | multi-configurational time-dependent Hartree |
| MD | molecular dynamics |
| ML | machine learning |
| MQCD | mixed quantum-classical dynamics |
| MR-ADC | multi-reference algebraic diagrammatic construction |
| MR-CC | multi-reference coupled cluster |
| MRCI | multi-reference configuration interaction |
| MRMP2 | multi-reference second-order Møller–Plesset perturbation theory |
| NAC | non-adiabatic coupling |
| NanoDOME | nanomaterials via gas-phase synthesis: a design-oriented modeling and engineering approach, H2020 project |
| NEVPT2 | N-Electron valence state second-order perturbation theory |
| ORMAS | occupation restricted multiple active space |
| OWVP | outgoing wave variational principle |
| PES | potential energy surfaces |
| PLDM | partial linearized density matrix |
| PW | pseudo-wavefunction |
| QD | quantum dynamics |
| QM | quantum mechanics |
| QMC | quantum Monte Carlo |
| QM/MM | quantum mechanics/molecular mechanics |
| RASPT2 | restricted active space second-order perturbation theory |
| RASSCF | restricted active space self-consistent field |
| REKS | spin-restricted ensemble-referenced Kohn–Sham |
| REW-TDDFT | restricted excitation window time-dependent density functional theory |
| RMProp | R-matrix propagation |
| RT | real-time |
| SA-SF-DFT | spin-adapted spin-flip density functional theory |
| SCF | self-consistent field |
| SC-SF-ORMAS | spin-complete spin-flip occupation restricted multiple active space |
| SE | stimulated emission |
| SF-ADC | spin-flip algebraic diagrammatic construction |
| SF-CIS | spin-flip configuration interaction singles |
| SF-DFT | spin-flip density functional theory |
| SimDOME | digital ontology-based modeling environment for simulation of materials, H2020 project |
| SI-SA-REKS | state-interaction with state-average spin-restricted ensemble-referenced Kohn–Sham |
| SOS | sum over all states |
| SR-CI | single-reference configuration interaction |
| TA | transient absorption |
| TDDFT | time-dependent density functional theory |
| TD-DMRG | time-dependent density matrix renormalization group |
| TDM | transition dipole moment |
| TRPES | time-resolved photoelectron spectroscopy |
| TRUECARS | transient redistribution of ultrafast electronic coherences in attosecond Raman signals |
| TSH | trajectory surface hopping |
| v2RDM | variational two-electron reduced-density matrix |
| vMCG | variational Multi-Configurational Gaussian wavepacket |
| WF | wavefunction |
| XMS-CASPT2 | extended multi-state complete active-space second-order perturbation theory |
Ultrafast Spectroscopy of Photoactive Molecular Systems from First Principles:
Where We Stand Today and Where We Are Going
Facebook
Twitter
Linkedin
Whatsapp
