
- Altmetric
Due to its unsurpassed capability to engage in various sp hybridizations or orbital mixings, carbon may contribute in expanding solid‐state nitrogen chemistry by allowing for different complex anions, such as the known NCN2− carbodiimide unit, the so far unknown CN3 5− guanidinate anion, and the likewise unknown CN4 8− ortho‐nitrido carbonate (onc) entity. Because the latter two complex anions have never been observed before, we have chemically designed them using first‐principles structural searches, and we here predict the first hydrogen‐free guanidinates TCN3 (T=V, Nb, Ta) and ortho‐nitrido carbonates T′ 2CN4 (T′=Ti, Zr, Hf) being mechanically stable at normal pressure; the latter should coexist as solid solutions with the stoichiometrically identical nitride carbodiimides and nitride guanidinates. We also suggest favorable exothermic reactions as useful signposts for eventual synthesis, and we trust that the decay of the novel compounds is unlikely due to presumably large kinetic activation barriers (C−N bond breaking) and quite substantial Madelung energies stabilizing the highly charged complex anions. While chemical‐bonding analysis reveals the novel CN4 8− to be more covalent compared to NCN2− and CN3 5− within related compounds, further electronic‐structure data of onc phases hint at their physicochemical potential in terms of photoelectrochemical water splitting and nonlinear optics.
Structural searches from first principles have led to the prediction of solid‐state carbodiimides, guanidinates, and ortho‐nitrido carbonates, the latter introducing the diamond motif into condensed‐matter nitrogen chemistry by high pressure. Some of these novel phases are expected to show potential in terms of photoelectrochemical water splitting and nonlinear optics.
Introduction
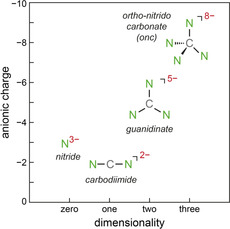
The search for new solid‐state nitrides or nitrogen‐based materials in general remains intense due to the wide range of exciting and quite diverse applications, such as N‐based fertilizers, explosives, high‐performance steel coatings, superconductors, electrides, UV‐LED materials, and a lot more. [1] Despite enormous promise in their chemical and physical functionalities, the sheer amount of N‐based materials is much smaller than those of the oxides, for reasons well known to chemists. [2] Somewhat simplified, the most fundamental N‐based anions which we dub “first generation” only contain nitrogen coordinated to a metal atom, such as simple nitrides, [3] pernitrides, [4] azides, [5] diazenides, [6] and the recently predicted LiN5. [7] The socalled “second generation” may then incorporate an additional nonmetal atom such as, for instance, in nitrido borates [8] or oxido nitrides. [9] Another prominent branch of the second generation is based, at least in principle, on C‐centered complex anions by utilizing the carbon atom's diverse hybridization (sp, sp2, sp3), thereby, for example, forming the linear carbodiimide or cyanamide NCN2− anion, see Figure 1. By doing so, the anionic dimensionality grows from zero (N3−) to one (NCN2−).

Sketch of charge and dimensionality of four nitrogen‐based (complex) anions as a function of their shape.
Clearly, N3− nitride and also NCN2− carbodiimide chemistries are well developed. Not only is GaN the fundamental material for blue light‐emitting diodes (LED), its chemistry started in the 1930s already [10] and was then extended, by Juza and successors, to practically all kinds of metals, growing ever since, now also covering metastable compounds such as Sn3N4 and Na3N. [11] As for carbodiimides, the earliest phase CaNCN served as a fertilizer in the 19th century and was structurally confirmed in 1962. [12] This field started to grow since the 1990s with better routes for main‐group metal carbodiimides. [13] After the turn of the millenium, transition‐metal carbodiimides also became accessible, [14] thereby opening up applications in (photo)electrochemistry. [15]
The next topological step consists of the planar (hence, two‐dimensional, see Figure 1) CN3 5− guanidinate anion, and a similar class of guanidinate phases was firmly established through making RbCN3H4 in 2011 [16] whose complex anion, descendant of the astonishingly basic guanidine molecule, still carries four N‐bonded H atoms. Syntheses in liquid ammonia further led to singly deprotonated (Li, Na, K, Rb, Cs, Ba, Eu) [17] and also doubly deprotonated (Sr, Ca, Yb) guanidinates [18] but a hydrogen‐free CN3 5− guanidinate unit has not been accomplished up to the present day. And yet, there should be the tetrahedral CN4 8− ortho‐nitrido carbonate (onc), a three‐dimensional complex anion (see Figure 1) which was never observed before, reminding us of the carbon atom's sp3 hybridization alluding to the diamond structure and a multitude of hydrocarbons or other CX4 species, thereby also highlighting the huge challenge to find such “tetrahedral” C‐based solid‐state compounds. [19]
To path the way to their discoveries, we have performed an extensive structure search based on structural evolution through the Particle Swarm Optimization (PSO) algorithm. [20] Assuming that the terminal structures and compositions have been firmly determined, the corresponding synthetic routes can then be adjusted by chemical creativity. For the density‐functional calculations, 3d‐5d transition metals of the vanadium group (V, Nb, Ta) were selected to satisfy charge balance given a fixed stoichiometry of TCN3. Likewise, the corresponding transition metals of the titanium group (Ti, Zr, Hf) were taken using a fixed T′ 2CN4 formula. Fortunately, we found twelve structurally and chemically related compounds which turned out as dynamically stable at atmospheric pressure, surprisingly enough. Among those, the first pure guanidinates TCN3 (T=V, Nb, Ta) were confirmed to contain the CN3 5− anion, and the first ortho‐nitrido carbonates T′ 2(CN4) (T′=Ti, Zr, Hf) were also predicted to incorporate CN4 8−. In addition, we found, somewhat unexpectedly, stable nitride carbodiimides of the form T′ 2N2(NCN) and nitride guanidinates T′ 2N(CN3) as predicted solid mixtures between N3− and NCN2− or CN3 5−, respectively, emphasizing the idea of solid‐state chemical equilibrium between those anions. All compounds are predicted as being semiconductors, and some of them should provide potential in the fields of electrochemical water splitting and nonlinear optics.
Results and Discussion
Stability
The PSO structure predictions were performed by running CALYPSO [21] based on density‐functional theory for unit cells containing up to four formula units TCN3 and T′ 2CN4, employing VASP together with projector augmented waves (PAW), [22] the generalized‐gradient approximation (GGA), [23] and the Monkhorst‐Pack scheme. [24] Twelve low‐energy compounds were studied in detail whose well optimized structural parameters are shown in Table S1. Their stability was confirmed by three criteria, namely, phonon band structure by finite displacements (Phonopy), [25] elastic constants, and synthetic route. That is to say that, first, all twelve phases are dynamically stable with no imaginary modes in the phonon bands (Figure S1), even at zero pressure. Second, as regards mechanical stability, the calculated elastic constants all satisfy the corresponding Born elastic stability criteria [26] as shown in Table S2. With respect to chemistry, the selected metathetic pathway for the composition TCN3 was chosen as [Eq. 1]
assuming convenient (i.e., high‐energy Na3N) starting materials. For the T′ 2CN4 composition, the metathetic route was targeted as [Eq. 2]
Fortunately, the negative formation energies shown in Figure S2 indicate that all TCN3 and T′ 2CN4 are exothermic phases, so successful synthesis should be tried. Other routes, better still, might be possible as well. Structurally, all TCN3 are predicted to crystallize in the hexagonal system with space group P c2 (see Figure 2) whereas, for T′ 2CN4, three different types of compounds should be observable, trigonal P m1, tetragonal P 21 c, and orthorhombic Cmc21 (see Figure 3), all three differing in and indicative of their chemical characters.

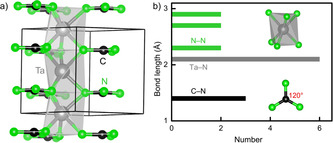
a) Crystal structure of TCN3 guanidinates (T=V, Nb, Ta) with space group P c2 and b) bond‐length histogram of various interactions.

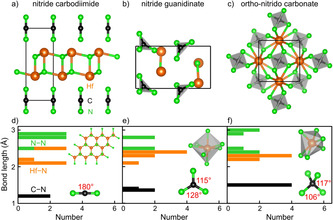
The crystal structures of the a) nitride carbodiimides, b) nitride guanidinates, and c) ortho‐nitrido carbonates of the T′ 2CN4 (T′=Ti, Zr, Hf) compositions using the Hf2CN4 example. The corresponding bond‐length histograms are given in d), e), and f).
Structural Details
Starting with the TCN3 types crystallizing in P c2, the compounds VCN3, NbCN3, and TaCN3 adopt the same structure as shown in Figure 2 a), and we select the heavy TaCN3 for a detailed internal description, see Figure 2 b). First, and in perfect harmony with the sum of Shannon's ionic radii for Ta5+ and N3−, [27] there are six equidistant Ta−N bonds of 2.10 Å inside a trans face‐sharing TaN6 octahedron stacked along c, a bit similar to the wider SrN6 octahedron (Sr−N=2.67 Å) in SrC(NH)3 but more twisted. [18] As for the important CN3 core with D 3h symmetry, there are no H atoms as in SrC(NH)3 while C−N=1.35 Å and N−C−N=120° are practically identical. [18] The shortest N−N distance of 2.35 Å is nonbonding, and Ta−Ta=2.8 Å is also far beyond the sum of the effective ionic radii for Ta5+ (0.64 Å), indicating essentially no N−N and Ta−Ta interactions. That being said, this first predicted transition‐metal guanidinate without H atoms appears as showing a “layered” motif with guanidinate anions and metal cations alternately stacked on top of each other, Figure 2 a).
As for the T′ 2CN4 formula, there are three different chemical motifs, corresponding to three different compound classes, and they are shown in Figures 3 a) to 3 c). For reasons of convenience, we select T′=Hf to study their chemical and structural peculiarities, as depicted in Figures 3 d) to 3 f). Similar to the previous discussion of TCN3, the shortest N−N distance of 2.32 Å and Hf−Hf distance of 2.97 Å are far beyond any significant interaction and will not be discussed any further. In contrast, the Hf−N and C−N bond lengths and connectivities help to separate the three different types of T′ 2CN4:
Figure 3 a) depicts the first P m1‐type T′ 2CN4 representative which is predicted to crystallize with two spatially separated Hf−N and N−C−N layers, a nitride carbodiimide T′ 2N2(NCN). There are three shortest Hf−N=2.09 Å bonds in a plane around each Hf4+ by nearest N3− neighbors to generate a heterographene‐like Hf−N layer, and two such layers form a double layer. For comparison, the Hf−N distances in Hf(NCN)2 lie between 2.03 and 2.24 Å. [28] The second shortest Hf−N=2.17 Å distance is the one connecting the upper and lower layers, see Figures 3 a) and 3 d). The third Hf−N=2.52 Å distance is essentially nonbonding. For the isolated carbodiimide unit, see Figure 3 d), there are two C−N=1.24 Å double bonds and a linear N=C=N shape, just as expected. In a sense, this crystal structure is topologically reminiscent of the recently reported bismuth oxide carbodiimide, Bi2O2(NCN), consisting of layers of [Bi2O2]2+ and [N=C=N]2−. [29] In addition, Bi2O2NCN has been confirmed suitable as a photoanode for photochemical water oxidation, just like the predicted T′ 2N2(NCN) as will be discussed later.
The second Cmc21‐type T′ 2CN4 candidate, depicted in Figure 3 b), is easily identified as a nitride guanidinate T′ 2N(CN3) but crystallizes with a lower symmetry than the previously predicted TCN3 guanidinates, mirrored by the irregular T′N7 decahedron and the slightly distorted planar CN3 5− anion, see Figure 3 e). The Hf−N distances in the HfN7 decahedron range from 2.09 to 2.34 Å, wider than before. As for the CN3 5− unit, the C−N bonds arrive at 2×1.35 Å and 1.40 Å, the angles being 115° and 128°, similar to Yb(CN3H4)3. [18]
Third, there is the primarily sought T′ 2CN4 class of phases crystallizing in P 21 c, given in Figure 3 c), the one that has never been observed before. In that crystal structure, Hf is coordinated by six N with 2×2.11 Å and 4×2.23 Å to form a distorted edge‐ and corner‐sharing HfN6 octahedron. The crucial CN4 8− unit, corresponding to an ortho‐nitrido carbonate (onc) anion, contains four identical C−N bonds of 1.49 Å, slightly larger than those of the known carbodiimides and guanidinates. Judged by the N−C−N angles of 106° and 117°, the onc unit is almost tetrahedral and conforms to D 2d symmetry, see Figure 3 f). We will further analyze the different chemical behavior to be expected from those differing structures.
Chemical Bonding and Electronic Structure
Because we are mostly interested in the behavior of the complex C/N‐based anions of the T′ 2CN4 formula, let us focus on them first. For the nearest intraionic C−N bonds (dubbed C−N1) listed in Figure 4 a), the bond lengths slightly increase as we go from nitride carbodiimides T′ 2N2(NCN) to nitride guanidinates T′ 2N(CN3) to onc T′ 2(CN4), a trivial function of the increasing coordination number of the central C atom; a similar course is not found for the T′−N distances. That is to say that the C−N1 bond slightly weakens but the larger number of C−N bonds upon going from carbodiimide (2) to guanidinate (3) to onc (4) must increase covalency as a whole. On the other side, there is a changing and likewise trivial trend of the T′−N distances, consistent with the changing ionic radii. If we take the onc structure, for example, in which T′ is sixfold coordinated, Shannon's ionic radii for such coordination are 0.61 Å for Ti4+, 0.72 Å for Zr4+, and 0.71 Å for Hf4+, [27] and the course runs parallel to what is found theoretically. In fact, the situation is a bit more complex because one finds two types of a T′−N bond, the slightly longer T′−N1 and slightly shorter T′−N2, Figure 3 f). For T′ 2N2(NCN) and T′ 2N(CN3), the T′−N1 distance is significantly longer than the T′−N2 distance, so the existence of the isolated N3− anion in T′ 2N2(NCN) and T′ 2N(CN3) is quite obvious even from geometry.

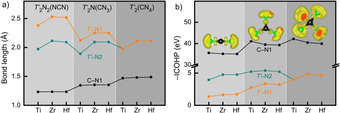
(a) Bond lengths and (b) integrated crystal orbital Hamilton population (ICOHP) of (the sum of) various bonds in T′ 2N2(NCN), T′ 2N(CN3), and T′ 2CN4. For simplicity, we designate C−N1 as the shortest C−N bond whereas T′−N1 is the shortest T′−N bond. The inset in (b) is the electron localization function (ELF) of anionic groups, with an isosurface level of 0.8.
The strengths of the chemical bonds are directly quantified by the Integrated Crystal Orbital Hamilton Populations (ICOHP) as projected by LOBSTER, [30] plotted in Figure 4 b). For T′ 2N2(NCN) and T′ 2N(CN3), the covalent part of the T′−N bonding is not too large, as expected for a metal‐nitrogen bond. As for the much more covalent and stronger intraionic C−N1 bond, the corresponding strength in the entire complex anions increases from carbodiimide to guanidinate to onc, see Figure 4 b), as a function of increasing condensation. This can also be illustrated in color by the socalled electron localization function (ELF) [31] of the N=C=N2−, CN3 5− and CN4 8− units (for T′=Hf), as displayed in Figure 4 b) using an isosurface level of 0.8. In the language of ELF, the clouds around the N atoms indicate “lone‐pair” electrons while the “localized” ones are visible, at least in principle, between C and N. ICOHP directly and numerically quantifies the higher covalency of the CN4 8− anion.
Questions of relative stability as a function of condensation (or volume) are most easily answered from energy‐volume plots. In order to do so, Vinet equations‐of‐state were calculated for Hf2N2(NCN), Hf2N(CN3), and Hf2CN4 to directly provide that information, see Figure 5 a). [32] It immediately turns out that, under standard conditions, the nitride carbodiimide Hf2N2(NCN) may be considered the most stable compound (see also convex‐hull discussion below), the chemical ground state, while the nitride guanidinate Hf2N(CN3) and the ortho‐nitrido carbonate Hf2CN4 are the metastable ones. As the pressure increases, see Figure 5 b), Hf2N2(NCN) will transform into Hf2N(CN3) at about 26 GPa and, at about 168 GPa, into Hf2CN4. On the other hand, it is puzzling that the spatial requirement of the different anions, as given at zero pressure, does not run parallel to the condensed nature of the complex anions. As seen from Figure 5 a), a nitride guanidinate is more densely packed than the onc while onc is still better packed than the nitride carbodiimide, so the mutual fit of the Hf−N bonds or the packing itself also must play a role. Given sufficient pressure, however, the nitride carbodiimide will condense into a nitride guanidinate, and a nitride guanidinate will condense into an ortho‐nitrido carbonate, so the highly covalent bonds eventually determine the effective volume.

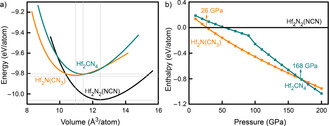
(a) Equation‐of‐state (EOS) fits for the total energies per atom as a function of volume for Hf2N2(NCN), Hf2N(CN3), and Hf2CN4; b) enthalpy‐pressure course of the three predicted compounds.
Before discussing other physical properties, two additional chemical questions must be answered, at least tentatively, as regards absolute thermochemical stability and chemical inertness under laboratory conditions. With respect to the first question, we have calculated possible decomposition pathways and theoretical phase diagrams (Figure S3). Confirming the prior arguments, Hf2N2(NCN) is the true ground state by −0.24 eV per Hf atom, thermodynamically stable against the convex hull, and should be straightforward to make. Surprisingly enough, Hf(NCN)2, [28] previously made by the Meyer group, turns out as being unstable by +0.08 eV. Its existence and strong inertness, even against water and air, points towards large activation barriers, a common phenomenon involving complex C/N‐containing anions (see below).
As regards Hf2N(CN3) and Hf2(CN4), they are prone to decay by +0.55 and +0.62 eV per Hf atom, whereas TaCN3 is unstable by +1.41 eV per Ta atom. That being said, the Ta phase is indeed less likely (but not impossible) whereas the two Hf phases would just need substantial kinetic barriers, larger than in the case of the known Hf(NCN)2. While we have been unable to carry out the necessary activation‐barrier calculations, partly due to the sheer complexity (far more complex than, say, the graphite‐diamond problem), partly due to our restricted computational facilities, other semiquantitative arguments are very much in favor of such large kinetic barriers. First, any decomposition of a carbodiimide, guanidinate, or ortho‐nitrido carbonate will involve C−N or C=N covalent bond breaking, on the order of 305–615 kJ mol−1 (3.2–6.4 eV), [33] and this is unlikely to begin with; this is also what makes diamond being inert for eternities. Second, electrostatic reasoning points into the same direction, as the LOBSTER‐calculated Madelung energies (per Hf atom) arrive at −31.9 eV for Hf2N2(NCN), −28.1 eV for Hf2N(CN3), and −32.0 eV for Hf2(CN4). Not only must these impressive energies be overcome for decomposition, they go back to the highly charged CN3 5− and CN4 8− anions and favor such densely packed high‐pressure phases. As a side note, we reiterate that the (even smaller) Madelung energy of Cr2(NCN)3 makes this unstable carbodiimide inert even at high temperatures as well as in acidic to alkaline media between pH 1–14. [14b]
This brings us to the second question targeting chemical stability which can only be answered experimentally. For example, some carbodimiides such as Hf(NCN)2, Cr2(NCN)3, PbNCN, etc. are perfectly inert in water,[ 14b , 28 , 34 ] sometimes simply due to surface passivation, others such as Li2NCN, Na2NCN, or CaNCN are not.[ 13a , 35 ] Hence, we truly need the experiment to corroborate the aforementioned signposts as regards activation barriers and to test the surface stability against a typical laboratory atmosphere.
Coming back to physical properties, the metal‐nonmetal interactions (i.e., covalent part of the Hf−N bonds) mirror what goes on between conduction and valence band, so they determine the band gap, as shown in the calculated densities of states (DOS) for Hf2N2(NCN), Hf2N(CN3) and Hf2CN4, given in Figure 6. Clearly, the nitrogen DOS spreads over the entire energy window through interaction with Hf and C, and the difference between an isolated N3− nitride and a C‐bonded nitrogen is easy to spot. As regards the band centers (shown as arrows on the right), the energetic proximity of Hf and N also indicates some covalent interactions in general, as already seen from COHP analysis, and the DOS shapes clearly broaden upon going from a) to b) to c), so the C−N covalency also strengthens and becomes maximized for the most condensed ortho‐nitrodo carbonate, as expected.

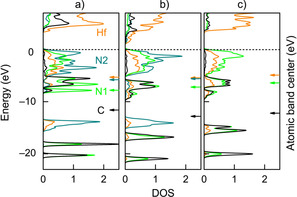
Calculated densities of states (DOS) for a) nitride carbodiimide Hf2N2(NCN), b) nitride guanidinate Hf2N(CN3), and c) ortho‐nitrido carbonate Hf2CN4. Orange, black and green lines represent Hf, C and N, respectively. Arrows on the right axis represent the atomic band centers below the Fermi level.
The hybrid functional HSE06 was chosen to arrive at the most reliable band‐gap values that are depicted in Figure 7. [36] For each composition and crystal structure, the band gap (grey and orange patterns) obviously increases with an increasing atomic number of the metal atom. It is straightforward to correlate this behavior with the course of the lowering Pauling electronegativities (Ti > Zr > Hf, and V> Nb > Ta), so the metal−N interactions become more ionic (larger band gap) upon going down each group of transition metals. What is puzzling, however, is the fact that the band‐gap character generally differs between the different classes of compounds. Clearly, the pure guanidinates TCN3 show the smallest band gaps, followed by the nitride guanidinates T′ 2N(CN3), then followed by the nitride carbodiimides T′ 2N2(NCN) and ortho‐nitrido carbonates T′ 2(CN4) which are comparable to each other.

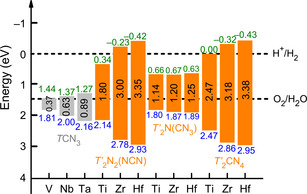
Calculated HSE06 band gaps for stable compounds of the composition TCN3 (T=V, Nb, Ta) and T′ 2CN4 (T′=Ti, Zr, Hf), the latter grouped into nitride carbodiimides, nitride guanidinates, and ortho‐nitrido carbonates. The band‐edge potentials are referenced to the reversible hydrogen electrode. Grey and orange colors indicate the band gap itself whereas green and blue colors represent the conduction band minimum (CBM) and valence band maximum (VBM), respectively.
Photochemical Water Splitting
Likewise, the band‐edge potentials were calculated with respect to the reversible hydrogen electrode (RHE), including the conduction band minimum (CBM) and the valence band maximum (VBM) estimated by the semiconductor electronegativity concept (Supporting Information), [37] see again Figure 7. The VBM and CBM of the nitride carbodiimides T′ 2N2(NCN) and the ortho‐nitrido carbonates T′ 2CN4 bracket the water redox energy range for T′=Zr and Hf, and for these elemental combinations they would achieve water splitting without any external bias voltage (EBV). The CBM of the other materials, however, locate under the H+/H2 energy level, indicating the necessary EBV for water splitting. On the other hand, the band‐gap value limits the type of light being harvested. As for T′=Zr and Hf, T′ 2N2(NCN) and T′ 2CN4 are the near ultraviolet (from 305 to 367 nm) light‐harvesting materials. As for the materials with a slightly too narrow band gap, thereby requiring a small EBV, that is, nitride carbodiimide Ti2N2(NCN) and onc Ti2CN4, they are capable to harvest the red (689 nm) and green light (502 nm), respectively. As such, the nitride carbodiimides T′ 2N2(NCN) and ortho‐nitrido carbonates T′ 2CN4 have been identified as potential candidates for water splitting. Especially for the first ones, the layered structures should turn out as particularly useful for making almost 2D‐like crystals, which would provide additional potential as multifunctional compounds. [38]
Nonlinear Optics
Within the ortho‐nitrido carbonates of the T′ 2(CN4) compounds, the complex CN4 8− anion itself comprises a large number of valence electrons (32) that may be shifted around and lead to electronic polarization. In combination with the tetrahedral character of this unit and a significant band gap, those onc compounds are therefore expected as being good candidates for nonlinear optical (NLO) applications, the NLO data calculated within modern polarization and density‐functional perturbation theory (DFPT) as implemented in ABINIT. [39] As for the visual spectrum from 400 to 700 nm, Ti2CN4 is predicted to show a second harmonic generation (SHG) coefficient of |d 36|=10.35 pm V−1 for the cutoff wavelength of λ=502 nm, which is comparable to the known AgGaS2 with d 36=13.0 pm V−1 for λ=454 nm. [40] As for the ultraviolet‐visible (UV/Vis) regime extending from 100 to 400 nm, T′ 2CN4 with T′=Zr and Hf have SHG coefficients of 3.96 and 2.62 pm V−1, with λ=390 and 367 nm, respectively. This is lower than for the known NLO phase BaGaS2 with 12.6 pm V−1 for λ=346 nm. [41] Nonetheless, onc‐type T′ 2CN4 with the distinct CN4 8− anion opens yet another NLO option in this field. In addition, the calculated birefringence shown in Table 1 is larger than 0.1, as derived from their refractive index (Figure S4).

|
|
λ (nm) |
SHG coefficients (pm V−1) |
Δn (nm) |
|---|---|---|---|
|
Ti2CN4 |
502 |
d 36=−10.35 |
0.123 |
|
Zr2CN4 |
390 |
d 36=−3.96 |
0.160 |
|
Hf2CN4 |
367 |
d 36=2.62 |
0.127 |
Mechanical Properties
For practical fabrication and device applications, the mechanical properties of the T′ 2CN4 composition which are computationally accessible by VASPKIT [42] must be studied (Table 2). For being brief, we here focus on the Hf compounds. Despite the sp3‐like carbon within ortho‐nitrido carbonate Hf2CN4, the calculated bulk modulus K=212 GPa and Young's modulus Y=250 GPa, indicating its resistant ability to compression and stiffness, are much smaller than diamond's sp3‐carbon (K=435, Y=1120 GPa), simply due to the much softer Hf−N bonds. The compound's universal elastic anisotropy A u=0.30, however, is close to that of diamond (0.27). In addition, the “softness” of the Hf−N interaction differs, as a function of the different chemical functionality, between the three types of compounds. For example, the negative Cauchy pressure or K/G<1.75 indicate the brittleness of the nitride guanidinate Hf2N(CN3). [43] The nitride carbodiimide Hf2N2(NCN) and the ortho‐nitrido carbonate Hf2CN4, however, are expected to show a more ductile behavior. Finally, the values of the minimum lattice thermal conductivity as derived from the elastic constants indicate the potential of all three compounds in terms of good thermal conductivity.

|
|
K |
G |
Y |
A u |
C |
K/G |
κ min |
|---|---|---|---|---|---|---|---|
|
Hf2N2(NCN) |
168 |
40 |
111 |
1.7 |
130 |
4.2 |
1.0 |
|
Hf2N(CN3) |
182 |
113 |
280 |
0.6 |
−44 |
1.6 |
1.4 |
|
Hf2(CN4) |
212 |
96 |
250 |
0.3 |
37 |
2.2 |
1.4 |
Conclusion
We have quantum‐mechanically predicted the existence of twelve stable transition‐metal compounds involving complex N‐based anions of dimensionality 1 to 3, including reasonable reaction pathways for their exothermic metathesis as well as high‐pressure approaches. As an obvious starting point, nitride carbodiimides such as Hf2N2(NCN) turn out as thermochemically stable and should be straightforward to synthesize. The more innovative types of those compositions are given by the first H‐free transition‐metal guanidinates TCN3 with T=V, Nb, Ta, and the ortho‐nitrido carbonates T′ 2CN4 with T′=Ti, Zr, Hf, the latter representing the most condensed and covalent ones of all. While being moderately unstable in terms of the convex hull, both covalent and ionic arguments are in strong favor of substantial kinetic barriers against their decay. In addition, the calculated electronic structures show that all twelve stable phases are semiconductors whose calculated band edges indicate Hf2CN4 to be the best candidates for photochemical water splitting, the nitride carbodiimides T′ 2N2(NCN) also showing good potential. Finally, the combined characters of strong C−N bond covalency, large band gap, and acentric symmetry suggests the ortho‐nitrido carbonates T′ 2CN4 as a novel type of NLO materials, with T′=Ti showing the highest SHG coefficient of 10.35 pm V−1.
Supporting Information. Computational details, calculated phonon band structures, formation energies of the exothermic reactions, convex‐hull discussion, Madelung energies and theoretical phase diagrams, birefringence, structural parameters and elastic constants of twelve compounds.
Conflict of interest
The authors declare no conflict of interest.
Acknowledgements
D.L. gratefully acknowledges expert help by the late Dr. Bernhard Eck for the technical support of the high‐performance cluster. Dr. Bernhard Eck passed away, aged 52, tragically and unexpectedly on August 14, so this work is meant in memoriam. We would also like to thank Peter Müller for help in the Madelung calculations. The simulation work is well‐supported by the IT center of RWTH Aachen University under grant JARA‐HPC (JARA0179). Open access funding enabled and organized by Projekt DEAL.
References
1
1a
1b
1c
1d
1f
2
3
3a
3b
3c
4
4b
4b
5
5a
5b
5b
5c
6
6a
6a
6b
6b
7
8
8
9
9a
9b
9c
10
10a
10b
10c
11
11a
11b
11c
11d
11d
12
12a
12b
13
13a
13b
14
14a
14b
14b
15
15a
15b
15b
17
17c
17d
17e
18
18a
18a
18b
18c
19
19a
19b
19c
19d
19e
20
21
22
22a
22b
22c
24
25
26
27
29
30
30a
30c
30d
30e
31
32
32a
32b
33
34
34a
34b
35
35a
35b
36
37
38
38a
38c
39
39a
39b
40
41
42
43
 Predicting Nitrogen‐Based Families of Compounds: Transition‐Metal Guanidinates TCN3 (T=V, Nb, Ta) and Ortho‐Nitrido Carbonates T′
2CN4 (T′=Ti, Zr, Hf)
Predicting Nitrogen‐Based Families of Compounds: Transition‐Metal Guanidinates TCN3 (T=V, Nb, Ta) and Ortho‐Nitrido Carbonates T′
2CN4 (T′=Ti, Zr, Hf)
